Question

A stone dropped from a tower reaches the ground after $4s$. If it was stopped $2$ seconds after its fall, and then released again, it would reach the ground after how many more seconds?
A. $\sqrt 7$
B. $\sqrt 8$
C. $\sqrt {12}$
D. $\sqrt 3$

Answer 1

When a body is dropped, it falls vertically downwards towards the ground to obey projectile motion. The acceleration due to gravity is considered to be constant throughout the fall, that is, at all points on its trajectory path. The heights of the body at the two given intervals of time are calculated and then the remaining height to be covered is hence found out. The equation for the time of flight of a body thrown vertically downwards is applied in order to obtain the time it will take to reach the ground.

Formula used:
The time of flight for the projectile falling vertically downwards is given by:
$T = \sqrt {\dfrac{{2h}}{g}}$
Where, $h$ is the height from which it falls and $g$ is the acceleration due to gravity.

Complete step by step answer:
The problem revolves around the concept of projectile motion. When a stone is dropped from a tower which has a height, it is said to fall towards the ground due to the gravitational pull of the Earth which makes the stone accelerate vertically downwards, that is, towards the pull. This stone during its fall from the tower is said to exhibit projectile motion.

Now, let us first look into the concept of projectile motion. Projectile is the name given to a body which once thrown into space moves with some initial velocity, and it exhibits motion thereafter under the influence of gravity alone without being propelled by any external force and this motion is known as projectile motion.

The trajectory of the body exhibiting projectile motion is said to be the path followed by the projectile. As per the question, the example taken here is the motion of the stone falling vertically downwards which means that the horizontal component or the motion of the stone in the horizontal direction is not considered. This is because there is no horizontal force being applied on it and the trajectory of the stone is vertically downwards.

For vertical motion, the initial velocity of the body is said to be zero since it is at rest and then it is dropped. From the equations of straight line of motion the equation for a straight line path is given as: $s = ut + \dfrac{1}{2}a{t^2}$
However, $u = 0$ over here and hence the equation becomes:
$s = (0) \times t + \dfrac{1}{2}a{t^2}$
$\Rightarrow s = 0 + \dfrac{1}{2}a{t^2}$
$\Rightarrow s = \dfrac{1}{2}a{t^2}$ -------($1$)
Here the distance covered by the projectile is nothing but the vertical distance of fall which would be equivalent to the height from which the stone is dropped. When a body exhibits projectile motion the time taken for the body to reach the ground is also considered which is said to be the time of flight of the body. It is defined as the total time for which the body remains in flight. The acceleration of the stone towards the ground is only due to the gravitational pull of the Earth.

Knowing this, let us denote the height of the tower as $h$, the time of flight of the stone as $T$ and the acceleration due to gravity is a constant value given as $g = 9.8m/{s^2}$.
Hence equation ($1$) becomes:
$\Rightarrow h = \dfrac{1}{2}g{T^2}$ --------($2$)
As our first step, we calculate the height from which the stone is dropped which is nothing but the height of the tower because when considering the first throw of the stone it is given that it falls directly down towards the ground without stopping it in between. Hence the distance covered or the trajectory of the stone will be equivalent to the height of the tower.

It is given in the question that the time taken to reach the ground is $4\sec$which is the time of flight. By substituting in the equation ($2$) given values we get:
$\Rightarrow h = \dfrac{1}{2} \times {(4)^2} \times 9.8$
By further solving the equation we get the total height of the tower:
$\Rightarrow h = \dfrac{1}{2} \times 16 \times 9.8$
$\Rightarrow h = 78.4\;m$

Now, we can see that it is given in the question that for the second throw of the stone, it is dropped then held for a few seconds and then released again. This means that the distance between the top of the tower and the point at which it is stopped will have a height and hence we now have to find out this height. The time of flight to cover this height is given to be $2\sec$.

The same equation that is equation ($2$) is applied here and we get:
$\Rightarrow h = \dfrac{1}{2} \times 9.8 \times {\left( 2 \right)^2}$
By further solving the equation we get:
$\Rightarrow h = \dfrac{1}{2} \times 9.8 \times 4$
$\Rightarrow h = 19.6\;m$
This is the height from the top of the tower till it reaches a point where it is stopped. We must now find the remaining height, that is, the remaining distance to be covered in order to reach the ground.

We have already found out the total height of the tower from the previous throw and we have also obtained the height from the tower to the point at which it was held and hence the remaining height to be calculated will be given by the difference between these two heights. This can be seen clearly in the below diagram:

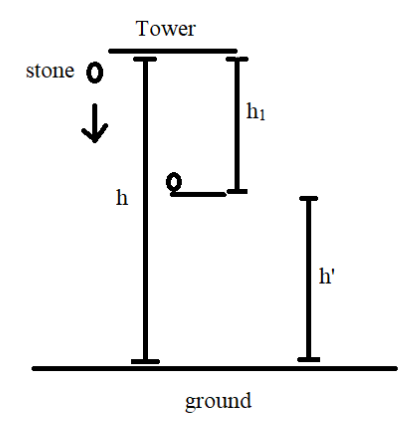
Here $h'$ denotes the remaining height. Hence as per the diagram the remaining height can be calculated by:
$h' = h - {h_1}$
By substituting the calculated values of height we get:
$\Rightarrow h' = 78.4 - 19.6$
$\Rightarrow h' = 58.8\;m$
Hence this is the remaining height which the stone must cover to fall to the ground.

However, we are asked to find out the time of flight of the stone to cover the remaining distance when it is released after $2$ seconds. Hence from equation ($2$) we get:
$\Rightarrow h = \dfrac{1}{2}g{T^2}$
By rearranging the terms we get:
$\Rightarrow {T^2} = \dfrac{{2h}}{g}$
Taking square root on both sides we get:
$\Rightarrow T = \sqrt {\dfrac{{2h}}{g}}$
Since the height considered here is the remaining height, $h'$ we get:
$\Rightarrow T = \sqrt {\dfrac{{2h'}}{g}}$ ---------($3$)
Hence in order to find the time of flight we substitute the obtained values and we get:
$\Rightarrow T = \sqrt {\dfrac{{2 \times 58.8}}{{9.8}}}$
$\Rightarrow T = \sqrt {\dfrac{{117.6}}{{9.8}}}$
$\therefore T = \sqrt {12}$
Hence the time of flight, that is, the time taken for the stone to reach the ground from the height it was released from after being held is $\sqrt {12} \sec$.

Hence the correct answer is option C.

Note: A common error made over here is that the difference in height will not be taken into consideration and usually direct substitution is made to find out the time of flight which is wrong. The time of flight for the remaining height needs to be determined. The conditions such as the air resistance and the effect due to the rotation of the Earth are considered to be negligible.