Question

A steel wire of cross-sectional area $3\times {{10}^{-6}}{{m}^{2}}$ can withstand a maximum strain of ${{10}^{-3}}$. If Young’s modulus of steel is $2\times {{10}^{11}}N{{m}^{-2}}$, then maximum mass which the wire can hold is (Take $g=10m{{s}^{-2}}$).
A.$40kg$
B.$100kg$
C.$80kg$
D.$60kg$

Answer 1

We shall analyze and calculate the force acting on the steel wire when a block of some mass, $m$hangs with it. Two forces act on this mass. One is the force of gravity in the downward direction and the other is the tension force acting the upward direction. Further, we shall study the relation of strain with Young’s modulus.

Complete answer:
The Young’s modulus is related to stress and strain as:
Young’s modulus, $Y=\dfrac{stress}{strain}$
Stress is the restoring force per unit area. It is the quantity which tells us how quickly the material will snap back (or restore) to its original orientation.
Strain is the change in length per length or the relative change in length. This quantity tells us how much the material has been deformed.
Stress $=\dfrac{F}{A}$ and Strain $=\dfrac{\Delta L}{L}$
Where,
$F=$ force applied on the object
$A=$ area of cross-section
$\Delta L=$ change in length due to application of force
$L=$ natural length of object
$\Rightarrow Y=\dfrac{\dfrac{F}{A}}{\dfrac{\Delta L}{L}}$
$\Rightarrow Y=\dfrac{FL}{A\Delta L}$
Thus, young’s modulus can also be expressed as:
$\Rightarrow Y=\dfrac{F}{A}\times \dfrac{1}{strain}$ ……………… equation (1)
The forces acting on the block of mass is:

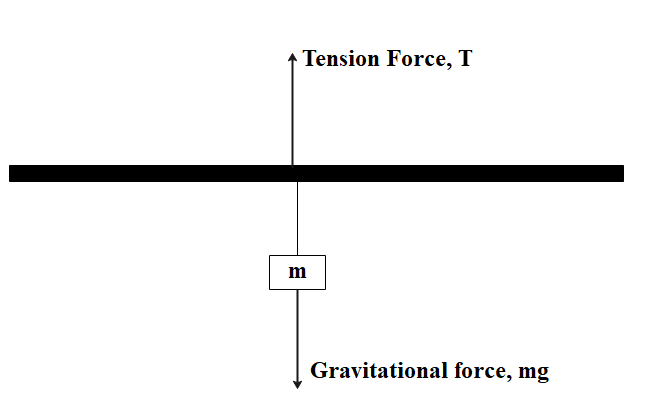
The force acting on the steel wire by the block, tension force, $T=mg$
Stress, $F=mg$
Substituting this value of force in equation (1),
$\Rightarrow Y=\dfrac{mg}{A}\times \dfrac{1}{strain}$
We are given that, maximum strain $={{10}^{-3}}$, $A=3\times {{10}^{-6}}{{m}^{2}}$, $Y=2\times {{10}^{11}}N{{m}^{-2}}$, and $g=10m{{s}^{-2}}$.
$\begin{aligned} & \Rightarrow 2\times {{10}^{11}}=\dfrac{m.10}{3\times {{10}^{-6}}}\times \dfrac{1}{{{10}^{-3}}} \\\ & \Rightarrow 2\times {{10}^{11}}\times 3\times {{10}^{-9}}=10m \\\ & \Rightarrow 6\times {{10}^{2}}=10m \\\ & \Rightarrow 600=10m \\\ \end{aligned}$
$\begin{aligned} & \Rightarrow m=\dfrac{600}{10} \\\ & \Rightarrow m=60kg \\\ \end{aligned}$
Hence, the maximum mass which the wire can hold is $60kg$.

Therefore, the correct option is (D) $60kg$.

Note:
Even in daily life, the various materials exhibiting elastic behaviour (like various wires around us) are constantly going under some stress and thus exhibiting strain. Strain is directly proportional to strain. The more force per unit area is applied to the elastic material (stress), the more is the material elongated or compressed per unit area (strain). This linear relationship is valid only until a particular limit after which the elastic material breaks off.