Question

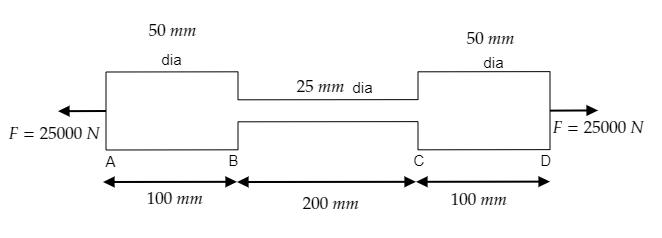
A steel bar ABCD $40{\text{cm}}$ long is made up of three parts AB, BC, and CD as shown in the figure. The rod is subjected to a pull of $25{\text{kN}}$. Find the extension of the rod. (Young’s modulus for steel is $2 \times {10^{11}}{\text{N}}{{\text{m}}^{ - 2}}$ ).
(dia means diameter in diagram)

A) $0.0637{\text{mm}}$
B) $0.0647{\text{mm}}$
C) $0.0657{\text{mm}}$
D) $0 0667{\text{mm}}$

Answer 1

The force applied for the extension of the rod will be experienced equally by all the three sections of the rod. The extension of the rod will be the sum of the extension of the three sections of the rod. So determining the stress of each part will help us to determine the change in length of the rod as the stress and strain are related by Young’s modulus of the material of the rod.

Formulas used:
i) The stress developed in a body is given by, $\sigma = \dfrac{F}{A}$ where $F$ is the force exerted on the body and $A$ is the area of the body.
ii) The longitudinal strain in a body is given by, $\varepsilon = \dfrac{{\Delta l}}{l}$ where $\Delta l$ is the change in length and $l$ is the original length of the body.
iii) Young’s modulus of a material is given by, $Y = \dfrac{\sigma }{\varepsilon }$ where $\sigma$ is the stress and $\varepsilon$ is the strain in the body.

Complete step by step answer:
Step 1: Sketch the given figure and list the parameters given.

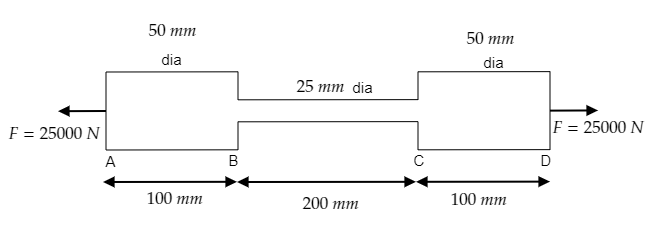
From the figure, we have the following parameters of the rod.
The length of part AB is ${l_{AB}} = 100{\text{mm}}$and its diameter is ${d_{AB}} = 50{\text{mm}}$ or its radius is ${r_{AB}} = 25{\text{mm}} = 0.025{\text{m}}$. Then its area will be ${A_{AB}} = \pi {r_{AB}}^2 = \pi {\left( {0.025} \right)^2}{{\text{m}}^2}$ .
The length of part BC is ${l_{BC}} = 200{\text{mm}}$ and its diameter is ${d_{BC}} = 25{\text{mm}}$ or its radius is ${r_{BC}} = 12.5{\text{mm}} = 0.0125{\text{m}}$. Then its area will be ${A_{BC}} = \pi {r_{BC}}^2 = \pi {\left( {0.0125} \right)^2}{{\text{m}}^2}$ .
The length of part CD is ${l_{CD}} = 100{\text{mm}}$ and its diameter is ${d_{CD}} = 50{\text{mm}}$ or its radius is ${r_{CD}} = 25{\text{mm}} = 0.025{\text{m}}$. Then its area will be ${A_{CD}} = \pi {r_{CD}}^2 = \pi {\left( {0.025} \right)^2}{{\text{m}}^2}$ .
The force applied to each part is the same.
i.e., ${F_{AB}} = {F_{BC}} = {F_{CD}} = 25000{\text{N}}$
Young’s modulus for steel is given to be $Y = 2 \times {10^{11}}{\text{N}}{{\text{m}}^{ - 2}}$.

Step 2: Express the stress of each part.
The stress developed in a body is generally expressed as $\sigma = \dfrac{F}{A}$ where $F$ is the force exerted on the body and $A$ is the area of the body.
Then for part AB, the stress will be ${\sigma _{AB}} = \dfrac{{{F_{AB}}}}{{{A_{AB}}}}$ ------- (1)
Substituting for ${F_{AB}} = 25000{\text{N}}$ and ${A_{AB}} = \pi {\left( {0.025} \right)^2}{{\text{m}}^2}$ in equation (1) we get the stress of part AB as ${\sigma _{AB}} = \dfrac{{25000}}{{\pi {{\left( {0.025} \right)}^2}}} = 1.273 \times {10^7}{\text{N}}{{\text{m}}^{ - 1}}$
Similarly, for part BC we have, ${\sigma _{BC}} = \dfrac{{{F_{BC}}}}{{{A_{BC}}}}$ ------- (2)
Substituting for ${F_{BC}} = 25000{\text{N}}$ and ${A_{BC}} = \pi {\left( {0.0125} \right)^2}{{\text{m}}^2}$ in equation (2) we get the stress of part BC as ${\sigma _{BC}} = \dfrac{{25000}}{{\pi {{\left( {0.0125} \right)}^2}}} = 5.092 \times {10^7}{\text{N}}{{\text{m}}^{ - 1}}$
And for part CD we have, ${\sigma _{CD}} = \dfrac{{{F_{CD}}}}{{{A_{CD}}}}$ ------- (3)
Substituting for ${F_{CD}} = 25000{\text{N}}$ and ${A_{CD}} = \pi {\left( {0.025} \right)^2}{{\text{m}}^2}$ in equation (3) we get the stress of part CD as${\sigma _{CD}} = \dfrac{{25000}}{{\pi {{\left( {0.025} \right)}^2}}} = 1. 273 \times {10^7}{\text{N}}{{\text{m}}^{ - 1}}$

Step 3: Express the change in length of each part to determine the extension of the rod.
The longitudinal strain in a body is given by, $\varepsilon = \dfrac{{\Delta l}}{l}$ where $\Delta l$ is the change in length and $l$ is the original length of the body.
Also, Young’s modulus of a material is given by, $Y = \dfrac{\sigma }{\varepsilon }$ where $\sigma$ is the stress and $\varepsilon$ is the strain in the body.
Combining these two relations we have, $Y = \dfrac{{\sigma l}}{{\Delta l}}$
$\Rightarrow \Delta l = \dfrac{{\sigma l}}{Y}$
For part AB we have, $\Delta {l_{AB}} = \dfrac{{{\sigma _{AB}}{l_{AB}}}}{Y}$ -------- (4)
On substituting for ${\sigma _{AB}} = 1. 273 \times {10^7}{\text{N}}{{\text{m}}^{ - 1}}$, ${l_{AB}} = 0. 1{\text{m}}$ and $Y = 2 \times {10^{11}}{\text{N}}{{\text{m}}^{ - 2}}$ in equation (4) we get the change in length of part AB as $\Delta {l_{AB}} = \dfrac{{1.273 \times {{10}^7} \times 0.1}}{{2 \times {{10}^{11}}}} = 6.365 \times {10^{ - 6}}{\text{m}}$
Since the stress and the length of parts AB and CD are the same, we have $\Delta {l_{CD}} = 6.365 \times {10^{ - 6}}{\text{m}}$ .
And for part BC we have, $\Delta {l_{BC}} = \dfrac{{{\sigma _{BC}}{l_{BC}}}}{Y}$ -------- (5)
On substituting for ${\sigma _{BC}} = 5.092 \times {10^7}{\text{N}}{{\text{m}}^{ - 1}}$, ${l_{BC}} = 0.2{\text{m}}$ and $Y = 2 \times {10^{11}}{\text{N}}{{\text{m}}^{ - 2}}$ in equation (5) we get the change in length of part BC as $\Delta {l_{BC}} = \dfrac{{5.092 \times {{10}^7} \times 0.2}}{{2 \times {{10}^{11}}}} = 5.092 \times {10^{ - 5}}{\text{m}}$
Now the extension of the rod is $\Delta l = \Delta {l_{AB}} + \Delta {l_{BC}} + \Delta {l_{CD}}$ --------- (6)
Substituting for $\Delta {l_{AB}} = \Delta {l_{CD}} = 6.365 \times {10^{ - 6}}{\text{m}}$ and $\Delta {l_{BC}} = 5.092 \times {10^{ - 5}}{\text{m}}$ in equation (6) we get, $\Delta l = \left( {6.365 \times {{10}^{ - 6}}} \right) + \left( {5.092 \times {{10}^{ - 5}}} \right) + \left( {6.365 \times {{10}^{ - 6}}} \right) = 6.37 \times {10^{ - 5}}{\text{m}}$
$\therefore$ the change in length of the rod is $\Delta l = 0.0637{\text{mm}}$.

So the correct option is (A).

Note: While substituting the values of physical quantities in any equation, make sure that all the quantities are expressed in their respective S.I. units. If this is not the case, then the necessary conversion of units must be done. Here the length and diameter (or radius) of the three sections of the rod were not expressed in millimetres so we converted these to meters before substituting in their values in the different equations.