Question
Question: A steel ball is dropped in a viscous liquid. The distance of the steel ball from the top of the liqu...
A steel ball is dropped in a viscous liquid. The distance of the steel ball from the top of the liquid is shown below. The terminal velocity of the ball is closest to:
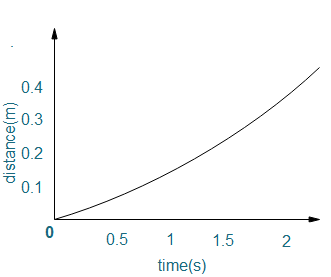
A. 0.26m/sB. 0.33 m/sC. 0.45 m/s
Solution
Terminal velocity is the maximum velocity of an object when falling through a liquid. Since, after attaining the terminal velocity, the velocity of the object becomes constant in a distance time graph the graph will be a straight line with constant slope. Find the part of the graph with constant slope and find the specific points of time and distance to find the required answer.
Complete step by step answer:
Terminal velocity of an object can be defined as the maximum velocity obtained by the object when it falls through a liquid.
When we draw a distance time graph for an object falling through a liquid, when the object reaches the terminal velocity, the graph should have a constant slope. This is because, after the terminal velocity is obtained by the object, the velocity of the object through the liquid will be constant.
In the given distance time graph in the question, the slope of the graph is constant for the time 1.6 second to 2 second.
When the time is 1.6 s, the distance covered by the object is 0.3 m and when the time is 2 s, the distance covered by the graph is 0.4 m.
So, the terminal velocity of the object found from the graph is,
Vt=2−1.60.4−0.3=0.40.1=0.25m/s
So, the terminal velocity of the object is approximately 0.26m/s.
So, the correct answer is “Option A”.
Note: The drag force on an object falling through a liquid is given by the Stokes’ law. Three forces act on a body falling through a liquid – the buoyant force, the drag force and the gravitational force. When we equate the downward gravitational force to the upward buoyant force and the drag force, we can find the terminal velocity of an object falling through liquid.
