Question
Question: A steady current is set up in a cubic network composed of wires of equal resistance and length d as ...
A steady current is set up in a cubic network composed of wires of equal resistance and length d as shown in the figure. What is the magnetic field at the center P due to the cubic network?
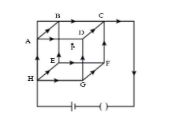
A. 4πμ0d2I
B. 4πμ02d3
C. 0
D. 4πμ02dθπI
Solution
Hint: In the given figure, the point P is at the center of the cubic network, so we can say that it is equidistant to all the wires forming the cubical network. First by applying Kirchhoff’s current law at every node of the cubical network, we will find out the current in each branch of the network given. Then, we can find the magnitude of magnetic field from a long straight wire at a point P at r distance from the wire by using the formula, B=2πrμ0I, where E is the magnetic field generated and I is the current in the wire.
Complete step by step solution:
We need to first find out the current flowing through each of the branches of the cubical network. For that, let us first consider that the initial current generated is i and as it reaches the node H, it gets divided into three branches HG, HE and HA. Since, it has been given that all the branches in the cubical network have equal resistances, so the current through each node will be divided equally.
So, we will apply Kirchhoff’s current law according to which at a node total current entering is equal to total current leaving that node. So, at node H total current entering is i and is getting distributed to branches HG, HE and HA all having equal resistances and thus will have equal currents in them that is 3i.
Similarly, upon applying Kirchhoff’s current law in nodes A, G and E, the current entering in them is 3i and as these nodes break into two similar branches, the current will be divided equally that is, 6i.
Hence, we can draw the following diagram after finding the value of current in all the branches of the cubical network
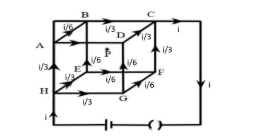
The next step to solve this question will be to derive the magnitude of magnetic field generated at a point placed in between two current carrying wire equidistant from each and having equal current and resistance. This can be depicted in the figure below,
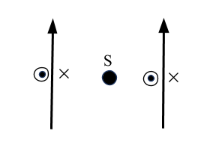
The point S is equidistant from the two wires having equal resistances and equal currents flowing in the same direction. So, let us suppose the point S is at a distance r from the two wires. So, the magnetic field generated at the point S from the two wires will be the same, that is 2πrμ0I but will have opposite directions. One will be into the plane and the other will be out of the plane. Thus, they will cancel out each other with 0 magnetic field at point S.
Similarly, we can apply this in the given question, where if we observe carefully, we will find that all the diagonally opposite sides have equal current flowing through them and thus all of them will generate equal magnetic fields at the point P ultimately cancelling each other out.
Hence option c is the right answer.
Note: The question looks a bit lengthier at first, but with clear understanding of the basics, we can easily find out the answer. The current division should be done carefully according to Kirchhoff's law or else we will not be able to find the answer correctly.
