Question

A steady current ‘i’ goes through a wire loop PQR having the shape of a right angled triangle with PQ = 3x, PR = 4x and QR = 5x. If the magnitude of magnetic field at P due to this loop is $k\left( \dfrac{\mu_{\circ}i}{48\pi x}\right)$, the value of k is?
A. 5
B. 8
C. 7
D. 10

Answer 1

The magnetic field due to a current carrying wire at some distance is given by Biot-Savart's law. Using this law, one can find the magnetic field values due to any number of wires. For using this law, one must know the shortest distance of the point to the wire which can be obtained by dropping a perpendicular from the point onto the wire.

Formula used:
$B = \dfrac{\mu_{\circ}i}{4\pi d}(sin \phi_1 + sin \phi_2)$

Complete answer:
We will proceed by understanding the formula $B = \dfrac{\mu_{\circ}i}{4\pi d}(sin \phi_1 + sin \phi_2)$. Here B is the net magnetic field due to current ‘i’ which is at a distance ‘d’. Note that the distance must be the shortest distance between the wire and point. $\phi_1 \ and \ \phi_2$ are the angles as shown in the figure.

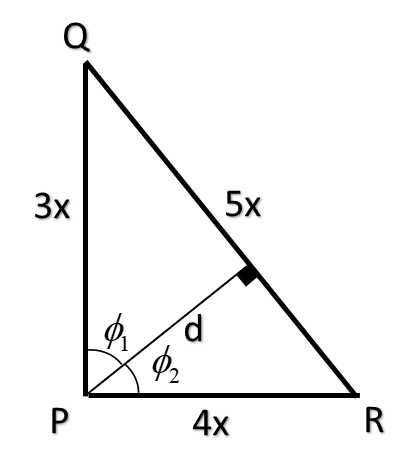
To find ‘d’, we will find the area in terms of ‘d’ i.e.
$Area \ = \ \dfrac 12 d\times 5x$
Also $area = \dfrac 12 4x\times 3x$
Hence, both must be equal:
$6x^2 = \dfrac 52 xd$
Or $d= \dfrac {12}5 x$
Now, from the figure, $cos \ \phi_1 = \dfrac {d}{3x} \ and \ cos \ \phi_2 = \dfrac{d}{x}$
Putting value of ‘d’, we get:
$cos \ \phi_1 = \dfrac {\dfrac {12}5 x}{3x} \ and \ cos \ \phi_2 = \dfrac{\dfrac{12}5 x}{4x}$
Or $cos \ \phi_1 = \dfrac 45 \ and \ cos \ \phi_2 = \dfrac {3}5$
Thus, $sin \ \phi_1 = \dfrac {{3}}5 \ and \ sin\ \phi_2 = \dfrac 45$
And $d= \dfrac {12}5 x$

Putting values in the equation:
$B = \dfrac{\mu_{\circ}i}{4\pi d}(sin \phi_1 + sin \phi_2)$
$B = \dfrac{\mu_{\circ}i}{4\pi {\dfrac{12}{5}x}}(\dfrac 35 + \dfrac 45)$
$B = \dfrac{5\mu_{\circ}i}{48\pi x} \times (\dfrac 75) = \dfrac{7\mu_{\circ}i}{48\pi x}$
Comparing this expression with the given equation, we get:
$k\left( \dfrac{\mu_{\circ}i}{48\pi x}\right) = \dfrac{7\mu_{\circ}i}{48\pi x} = 7 \left(\dfrac{\mu_{\circ}i}{48\pi x} \right)$
Hence $k=7$.

So, the correct answer is “Option c”.

Note:
One might wonder that the current is also passing through sides PQ and RP. Why don’t we consider the magnetic field due to this part of the frame? This is because in case if the point is lying on the wire frame or the point and the wire lie in the same line, the angle $\phi_1$ becomes 0 and angle $\phi_2$ becomes $180^\circ$. Hence the overall field due to PQ and RP becomes zero and only the field due to QR is considered.