Question

A steady current $I$ goes through a wire loop $PQR$ having the shape of a right angle triangle with $PQ = 3x$, $PR = 4x$ and $QR = 5x$. If the magnitude of the magnetic field at $P$ due to this loop is $k\left( {\dfrac{{{\mu _0}T}}{{48\pi }}} \right)$, find the value of $k$.

Answer 1

Hint: The wire loop $PQR$ forms a right-angled triangle. When the current flows through the loop it generates a magnetic field around it. When the current flows through the loop $PR$ and $PQ$, the magnetic field at the point $P$ is zero. While passing through loop $QR$, it generates the magnetic field at point $P$. Firstly, the right angled triangle $PQR$ is split up into two right angled triangles $PQD$ and $PDR$. And by using the area formula the value of $PD$ is obtained. With the help of Pythagoras theorem, the value of $QD$ is obtained. And the value of $DR$ is calculated by subtracting $QD$ from $QR$. Substituting all the values in the magnitude of the magnetic field, the values of k will be derived.

Useful formula:
Area of the triangle = $\dfrac{1}{2}bh$
Where, $b$ is the breadth of triangle and $h$ is the height of the triangle.

Magnitude of magnetic field, $B = \dfrac{{{\mu _0}I}}{{4\pi r}}\left( {\sin {\theta _1} + \sin {\theta _2}} \right)$
Where, ${\mu _0}$ is the permeability of free space, $I$ is the current flowing normal to the point, $r$ is the perpendicular distance between the point and current flowing and ${\theta _1}$, ${\theta _2}$ are referred in the diagram given above.
Given data:
$PQ = 3x$
$PR = 4x$
$QR = 5x$
The magnitude of magnetic field, $B = k\left( {\dfrac{{{\mu _0}I}}{{48\pi x}}} \right)$

Step by step solution:

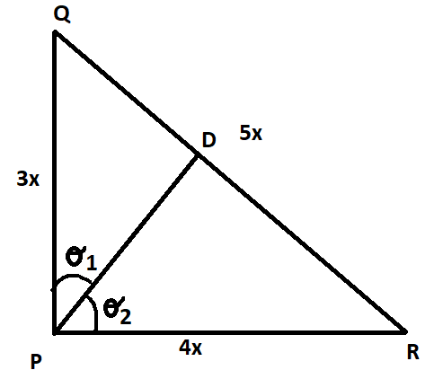
By the properties of area of triangle,
$\dfrac{1}{2} \times PD \times QR = \dfrac{1}{2} \times PR \times PQ$
Substitute the above values, we get
$\dfrac{1}{2} \times PD \times 5x = \dfrac{1}{2} \times 4x \times 3x \\\ PD = \dfrac{2}{{2\left( {5x} \right)}} \times 4x \times 3x \\\ PD = \dfrac{{12x}}{5} \\\$

By Pythagoras theorem,
$QD = \sqrt {{{\left( {PQ} \right)}^2} - {{\left( {PD} \right)}^2}}$
Substitute the given values, we get
$QD = \sqrt {{{\left( {3x} \right)}^2} - {{\left( {\dfrac{{12x}}{5}} \right)}^2}} \\\ QD = \sqrt {\left( {9{x^2}} \right) - \dfrac{{144{x^2}}}{{25}}} \\\ QD = x \times \sqrt {9 - \dfrac{{144}}{{25}}} \\\ QD = x \times \sqrt {\dfrac{{\left( {225 - 144} \right)}}{{25}}} \\\ QD = x \times \sqrt {\dfrac{{81}}{{25}}} \\\ QD = x \times \dfrac{9}{5} \\\ QD = \dfrac{{9x}}{5} \\\$
Hence, $DR = QR - QD$
$DR = 5x - \dfrac{{9x}}{5} \\\ DR = \dfrac{{\left( {25x - 9x} \right)}}{5} \\\ DR = \dfrac{{16x}}{5} \\\$

When the current passes through $PQ$ and , the value of magnetic field at $P$ will be zero. Because the current passes through the point itself. And when the current flows through $QR$, the magnetic field at $P$ will be
$B = \dfrac{{{\mu _0}I}}{{4\pi \times PD}}\left( {\sin {\theta _1} + \sin {\theta _2}} \right) \\\ B = \dfrac{{{\mu _0}I}}{{4\pi \times PD}}\left( {\dfrac{{QD}}{{QP}} + \dfrac{{DR}}{{PR}}} \right) \\\$
Substitute the given values, we get
$B = \dfrac{{{\mu _0}I}}{{4\pi \times \left( {\dfrac{{12x}}{5}} \right)}}\left( {\dfrac{{\left( {\dfrac{{9x}}{5}} \right)}}{{3x}} + \dfrac{{\left( {\dfrac{{16x}}{5}} \right)}}{{4x}}} \right) \\\ B = \dfrac{{{\mu _0}I \times 5}}{{4\pi \times 12x}}\left( {\dfrac{3}{5} + \dfrac{4}{5}} \right) \\\ B = \dfrac{{{\mu _0}I \times 5}}{{4\pi \times 12x}}\left( {\dfrac{7}{5}} \right) \\\ B = \dfrac{{{\mu _0}I \times 7}}{{48\pi x}} \\\ B = 7\left( {\dfrac{{{\mu _0}I}}{{48\pi x}}} \right) \\\$
By comparing the given value of $B$ and the above derived value of $B$, we get $k = 7$

Note: Since, the perpendicular distance between the point and the current flow will be zero. Thus, the magnetic field at a point will be zero when the current flows through the same point. The area of the right-angled triangle can be obtained by two different ways shown above. The magnetic field induced will decrease when the perpendicular distance tends to increase.