Question

A steady current $I$ goes through a wire loop PQR having a shape of right angle triangle with PQ=3x, PR=4x and QR=5x. If the magnitude of magnetic field at P due to this loop is $k\left( {\dfrac{{{\mu _0}I}}{{48\pi x}}} \right)$. Find the value of $k$.
A. $9$
B. $5$
C. $10$
D. $7$

Answer 1

Determine the values of the altitude of the right angle triangle and the distances of the hypotenuse divided by the altitude. Determine the values of sine of angles made by the altitude from a vertex of the triangle with the other two sides of the right angle triangle. Substitute these values in the formula for magnetic field for a right angel triangle.

Formulae used:
The area of a triangle is
${\text{Area of triangle}} = \dfrac{1}{2} \times {\text{base}} \times {\text{height}}$ …… (1)
The area of a right angled triangle is
${\text{Area of triangle}} = \dfrac{1}{2} \times {\text{altitude}} \times {\text{hypotenuse}}$ …… (2)
The magnetic field at a point P on the vertex of the right angle triangle is given by
The area of a triangle is
$B = \dfrac{{{\mu _0}I}}{{4\pi \left( {{\text{altitude of triangle}}} \right)}}\left( {\sin {\theta _1} + \sin {\theta _2}} \right)$ …… (3)
Here, is the permeability of free space, is the current and are the angles made by the altitude of the triangle from one of the vertices with the two sides of the right angle triangle.

Complete step by step answer:
We have given that a steady current $I$ goes through a wire loop PQR having a shape of right angle triangle with PQ=3x, PR=4x and QR=5x. Let us first draw the diagram for the wire loop POR.

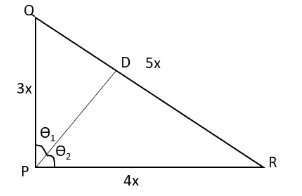
In the above diagram, PD is the altitude of the right angled triangle. The angle made by the altitude of this triangle with the sides PQ and PR of the right angle triangle are ${\theta _1}$ and ${\theta _2}$ respectively.

The area of the triangle PQR is given by using equations (1) and (2).
${\text{Area of triangle}} = \dfrac{1}{2} \times {\text{PR}} \times {\text{PQ}}$
Substitute $4x$ for ${\text{PR}}$ and $3x$ for ${\text{PQ}}$ in the above equation.
${\text{Area of triangle}} = \dfrac{1}{2} \times 4x \times 3x$
$\Rightarrow {\text{Area of triangle}} = 6{x^2}$
And
${\text{Area of triangle}} = \dfrac{1}{2} \times {\text{PD}} \times {\text{QR}}$
Substitute $5x$ for ${\text{QR}}$ in the above equation.
${\text{Area of triangle}} = \dfrac{1}{2} \times {\text{PD}} \times 5x$
Equate these two areas of the triangles.
$\dfrac{1}{2} \times {\text{PD}} \times 5x = 6{x^2}$
$\Rightarrow {\text{PD}} = \dfrac{{12x}}{5}$

Now we can determine the length of QD using Pythagoras theorem.
${\text{P}}{{\text{Q}}^{\text{2}}} = {\text{P}}{{\text{D}}^{\text{2}}} + {\text{Q}}{{\text{D}}^{\text{2}}}$
Substitute $3x$ for ${\text{PQ}}$ and $\dfrac{{12x}}{5}$ for ${\text{PD}}$ in the above equation.
${\left( {3x} \right)^{\text{2}}} = {\left( {\dfrac{{12x}}{5}} \right)^{\text{2}}} + {\text{Q}}{{\text{D}}^{\text{2}}}$
$\Rightarrow {\text{Q}}{{\text{D}}^{\text{2}}} = 9{x^2} - \dfrac{{144{x^2}}}{{25}}$
$\Rightarrow {\text{QD}} = \dfrac{{9x}}{5}$

The length of the side QR is the sum of the lengths QD and DR.
${\text{QR}} = {\text{QD}} + {\text{DR}}$
Substitute $5x$ for ${\text{QR}}$ and $\dfrac{{9x}}{5}$ for ${\text{QD}}$ in the above equation.
$5x = \dfrac{{9x}}{5} + {\text{DR}}$
$\Rightarrow {\text{DR}} = \dfrac{{16x}}{5}$

The sine of an angle in a right angle triangle is the ratio of the side opposite to that of the angle and hypotenuse.
Hence, the value of angles ${\text{sin}}{\theta _1}$ and ${\text{sin}}{\theta _2}$ is
${\text{sin}}{\theta _1} = \dfrac{{{\text{QD}}}}{{{\text{PQ}}}}$
$\Rightarrow {\text{sin}}{\theta _1} = \dfrac{{\dfrac{{9x}}{5}}}{{3x}}$
$\Rightarrow {\text{sin}}{\theta _1} = \dfrac{9}{{15}}$
And
${\text{sin}}{\theta _2} = \dfrac{{{\text{DR}}}}{{{\text{PR}}}}$
$\Rightarrow {\text{sin}}{\theta _2} = \dfrac{{\dfrac{{16x}}{5}}}{{4x}}$
$\Rightarrow {\text{sin}}{\theta _2} = \dfrac{{16}}{{20}}$

Let us determine the value of the magnetic field.
Substitute ${\text{PD}}$ for ${\text{altitude of triangle}}$ in equation (3).
$B = \dfrac{{{\mu _0}I}}{{4\pi \left( {{\text{PD}}} \right)}}\left( {\sin {\theta _1} + \sin {\theta _2}} \right)$
Substitute $\dfrac{{12x}}{5}$ for ${\text{PD}}$, $\dfrac{9}{{15}}$ for $\sin {\theta _1}$ and $\dfrac{{16}}{{20}}$ for $\sin {\theta _2}$ in the above equation.
$B = \dfrac{{{\mu _0}I}}{{4\pi \left( {\dfrac{{12x}}{5}} \right)}}\left( {\dfrac{9}{{15}} + \dfrac{{16}}{{20}}} \right)$
$\Rightarrow B = \dfrac{{5{\mu _0}I}}{{48\pi x}}\left( {\dfrac{{180 + 240}}{{300}}} \right)$
$\Rightarrow B = \dfrac{{{\mu _0}I}}{{48\pi x}}\left( {\dfrac{{420}}{{60}}} \right)$
$\therefore B = 7\left( {\dfrac{{{\mu _0}I}}{{48\pi x}}} \right)$
From the above equation, we can conclude that the value of k is 7.

Hence, the correct option is D.

Note: The same question can be solved by another method. If one considers the angles made by the remaining angles of the right angle triangle other than the right angle then the formula for magnetic field used will be the same. The only thing we need to change is to take the cosine of these angels instead of sine of the angles.