Question
Question: A statue 4 meters high sits on a column 5.6 meters high. How far from the column must a man, whose e...
A statue 4 meters high sits on a column 5.6 meters high. How far from the column must a man, whose eye level is 1.6 meters from the ground, stand in order to have the most favorable view of the statue.
Solution
First, draw the figure on the base of data provided. Then find the value of tanβ from triangle BCD. After that, find the value of tanα from the triangle ABC by using formula tan(A+B)=1−tanAtanBtanA+tanB. After that differentiate the terms with respect to x and equate with 0 to maximize the function for a favorable view. Then solve for x.
Complete step-by-step answer:
To find:- The distance between the column and man.
Let the distance between the column and man be x.
The figure for the problem is,
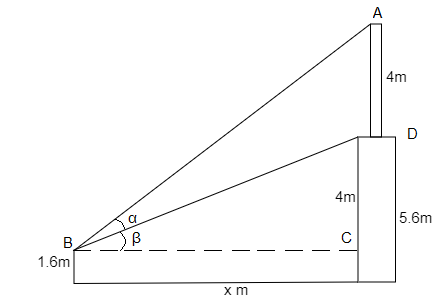
In ΔBCD,
tanβ=BCBD
Substitute the value of BD and BC,
tanβ=x4 ….. (1)
In ΔABC,
tan(α+β)=BCAC
Since AC=AD+DC. Then,
tan(α+β)=BCAD+DC
Substitute the values of AD, DC, and BC,
tan(α+β)=x4+4
As we know that tan(A+B)=1−tanAtanBtanA+tanB. So,
1−tanαtanβtanα+tanβ=x8
Substitute the value of tanβ from equation (1),
1−tanα×x4tanα+x4=x8
Multiply the denominator of the left side on the right side,
tanα+x4=x8−x232tanα
Move x232tanα on the left side and x4 on the right side,
tanα+x232tanα=x8−x4
Take tanα common from the left side and subtract the terms on the right side,
tanα(1+x232)=x4
Divide both sides by (1+x232),
tanα=(1+x232)x4
Take LCM in the denominator,
tanα=(x2x2+32)x4
Cancel out the common factors,
tanα=x2+324x
For the most favorable view, we have to maximize θ. Since θ∈(0,2π].
Let t(x)=tanθ,
t(x)=x2+324x
Differentiate with respect to x.
dxd[t(x)]=dxd(x2+324x)
As we know that, dxd[g(x)f(x)]=[g(x)]2g(x)f′(x)−f(x)g′(x). Then,
dxd[t(x)]=(x2+32)2(x2+32)×4−4x(2x)
Open the brackets and multiply the terms. For maximum substitute dxd[t(x)]=0.
(x2+32)24x2+128−8x2=0
Subtract the like terms in the numerator and multiply the denominator to the right side,
128−4x2=0
Move the variable on the other side,
4x2=128
Divide both sides by 4,
x2=32
Take the square root on both sides,
x=±32
Since, distance cannot be negative,
x=42m
Hence, the distance between the column and man is 42m.
Note: The ratio should exist between the quantities of the same kind.
While comparing two things, the units should be similar.
There should be significant order of terms.
The comparison of two ratios can be performed, if the ratios are equivalent to the fractions.
