Question

A statue 1.6m long stands on the top of the pedestal. From a point on the ground, the angle of elevation of the top of the statue is ${{60}^{o}}$ and from the same point the angle of the elevation of the top of the pedestal is ${{45}^{o}}$ . Find the height of the pedestal.

Answer 1

Hint: The given problem is related to heights and distances. Using the information given, construct the diagram. In the triangles, use trigonometric ratios of tangent of an angle to find the height of the pedestal.

Complete step by step answer:

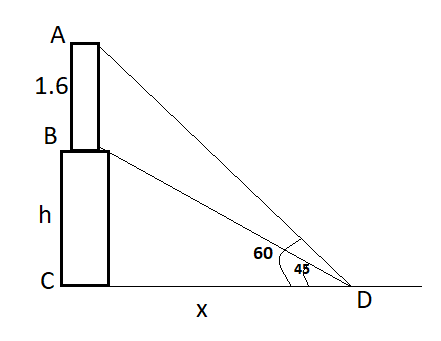
In this diagram:
BC = height of the pedestal = h;
AB= height of the statue = 1.6m;
CD=distance between the base of pedestal to the point .
The angle of elevation to the top of the statue is ${{60}^{\circ }}$
The angle of elevation to the top of pedestal is ${{45}^{\circ }}$

Let's consider CD=x.

We will apply ‘tan’ in $\Delta BCD$ at D: $$\Rightarrow tan45\text{ }=\text{ }\dfrac{BC}{CD}=\text{ }\dfrac{h\text{ }}{x};$$
$\Rightarrow 1=\text{ }\dfrac{h\text{ }}{x};$

\Rightarrow h\text{ }=\text{ }x;~~$$$$.......(1)
Now, we will apply ‘tan’ in $\Delta ACD$at D :

$\Rightarrow \tan {{60}^{\circ }}=\dfrac{AC}{CD}=\dfrac{\left( \text{ }h+1.6 \right)}{x}\text{ };$
\Rightarrow \sqrt{3}=\dfrac{\left( \text{ }h+1.6 \right)}{x}\text{ };$$$$.......(2)

Now, we will substitute x = h in equation 2;
Then equation 2 becomes:

$\Rightarrow \sqrt{3}h\text{ }=\text{ }h\text{ }+1.6$
Now, as h is the variable, we will take all terms with h to one side. Equation becomes:

$\Rightarrow (\sqrt{3}-1)h\text{ }=1.6$
$\Rightarrow h\text{ }=\text{ }\dfrac{1.6}{\sqrt{3}-1}$
$\Rightarrow h\text{ }=\text{ }\dfrac{1.6}{1.732-1}$
$\Rightarrow h\text{ }=\text{ }\dfrac{1.6}{0.732}$
$\Rightarrow h\text{ }=\text{ 2}\text{.1858}$

Therefore, the height of the pedestal in the given question is 2.1858m.

Note: The way of understanding the question is very important. So, illustrate the diagram carefully without confusing the question which gives you the major idea to solve the problem solving.