Question

A statue 1.46 m tall stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is ${60^o}$ and from the same point the angle of elevation of the top of the pedestal is ${45^o}$. Find the height of the pedestal [Use$\sqrt 3 = 1.73$]

Answer 1

The problem can be solved by using trigonometry. The formula for the tangent of the angle should be used 2 times. Tangent of an angle is given by, $\tan \theta = \dfrac{P}{B}$, where P = perpendicular and B = base of the right triangle.

Complete step-by-step answer:
The figure according to the condition given in the question is as follows,

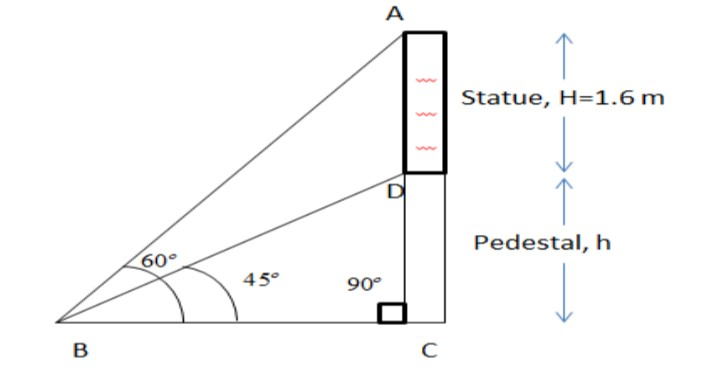
In right triangle, DBC right angled at C
$\tan {45^o} = \dfrac{P}{B} = \dfrac{h}{{BC}}$
The value of $\tan {45^o} = 1$
$\Rightarrow \dfrac{h}{{BC}} = 1 \\\ h = BC......(1) \\\$

In right triangle, ABC right angled at C
$\tan {60^o} = \dfrac{P}{B} \\\ \tan {60^o} = \dfrac{{AC}}{{BC}} \\\ \tan {60^o} = \dfrac{{h + 1.46}}{{BC}} \\\$

The value of $\tan {60^o} = \sqrt 3$
$\Rightarrow \dfrac{{h + 1.46}}{{BC}} = \sqrt 3$
$\dfrac{{h + 1.46}}{h} = \sqrt 3 ......(2)$

Substitute h = BC in equation (2)
$h + 1.46 = h\sqrt 3 ......(3)$

The value of $\sqrt 3 = 1.73$ as per the question, substitute it in equation (3)
$h + 1.46 = 1.73h \\\ 1.73h - h = 1.46 \\\ 0.73h = 1.46 \\\ h = \dfrac{{1.46}}{{0.73}} \\\ h = 2 \\\$
Hence, the height of the pedestal is, $h = 2$ m.

Note: The figure should be drawn very carefully and the angle should be marked appropriately.
The value of the tangent of the angle should be remembered.