Question
Question: A stationary person observes that rain is falling vertically down at 30km/hr. A cyclist is moving up...
A stationary person observes that rain is falling vertically down at 30km/hr. A cyclist is moving up on an inclined plane making an angle 300with horizontal at 10km/hr. In what direction should the cyclist hold his umbrella to prevent himself from rain?
A) At an angle of tan−1(533)with the inclined plane
B) At an angle of tan−1(73)with the inclined plane
C) At an angle of tan−1(533)with the horizontal
D) At an angle of tan−1(73)with the vertical
Solution
Hint: The velocity of rain for a stationary observer VR and the velocity of the man VM are given. We have to find their relative velocity and calculate the angle subtended by them with the vertical. It is given that the rider is in an inclined plane of 300. Using these relations we have to evaluate which of the following is true.
Formula used:
VAB=VA−VB, where VAB is the velocity of A with respect to B , VAis the velocity of A and VB is the velocity of B.
tan(x−y)=1+tanxtanytanx−tany
Complete step by step answer:
Let us start by mentioning the details given in the question. It is given that VR=−30j^. VM can be divided into its components in x and y direction. It has a magnitude of 10km/hr and makes an angle of 300. Therefore VM=2103i^+210j^
UsingVAB=VA−VB, where VABis the velocity of A with respect to B, VA is the velocity of A and VB is the velocity of B we get
VRM=VR−VM
VRM=−30j^−(2103i^+210j^)
VRM=53i^−35j^
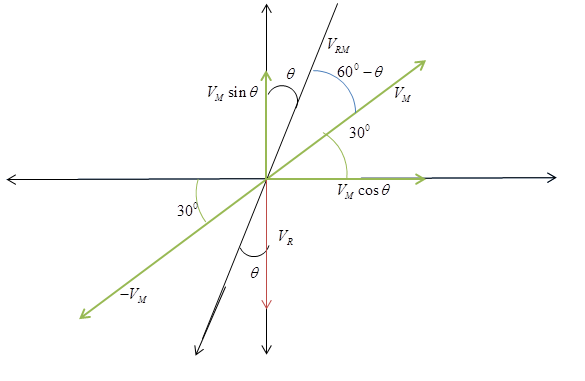
tanθ=3553=73
θ=tan−1(73)
θ is the angle formed between VRM and the vertical line.
Therefore cyclist should hold his umbrella at an angle of tan−1(73)with the vertical to prevent himself from rain.
From the diagram we can see that the angle it makes with the inclined plane (let say β) is equal to 600−θ, since θ+β+300=900
Therefore using tan(x−y)=1+tanxtanytanx−tany
tan(600−θ)=1+tan600tanθtan600−tanθ
tanθ=73
tan(β)=1+3×733−73
tan(β)=710763
tan(β)=533
β=tan−1533
β is the angle formed between VRM and the inclined plane. Therefore cyclist should hold his umbrella at an angle of tan−1(533)with the inclined plane to prevent himself from rain.
Both the options (A) and (D) are correct.
Note: It is important to note where the angles are formed between in order to answer properly.
When the magnitude A and angle θformed in x axis is given it is usually represented as the sum of its components in x and y direction. I.e. Acosθi^+Asinθj^.
