Question

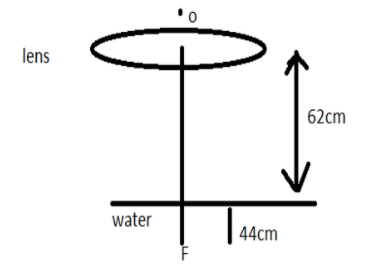
A stationary observer O looking at a fish (in water of $\mu =\dfrac{4}{3}$) through a converging lens of focal length $90.0cm$. The lens is allowed to fall freely from height of $62.0cm$ with its axis vertical. The fish and the observer are on the principal axis of the lens. The fish moves up with constant velocity $100m{{s}^{-1}}$. Initially, it was a depth of $44.0cm$. Find the velocity with which the fish appears to move to the observer at $t=0.2\sec$.

A. $12.75cm/s$ (upwards)
B. $22.75cm/s$ (upwards)
C. $29.75cm/s$ (upwards)
D. $52.75cm/s$ (upwards)

Answer 1

We have to find the velocity with which the fish appears to move to the observer at time $0.2\sec$. The reciprocal of the focal length will be equivalent to the sum of the reciprocal of the object distance and the reciprocal of the image distance.

Complete step by step solution:
As given above that a stationary observer looking O looking at a fish through the converging lens of focal length $90.0cm$. The lens is allowed to fall freely from the height of $62.0cm$ with its axis vertical. The fish and the observer are on the principal axis of the lens. The fish moves up with constant velocity $100m{{s}^{-1}}$. Initially it was a depth of $44.0cm$.

Now as if to find the velocity with which the fish assumes to moves to the observer at,
At $t=0.2\sec$
Velocity of lens,
${{V}_{1}}=gt$ eq. (1)
Where$g$ is the gravitational force and $t$ is the given time.
Hence, ${{V}_{1}}=10\times 0.2$
$\Rightarrow {{V}_{1}}=2m/s$(Downwards)

For lens, the speed with which the fish appears to approach is,
$2+(1\times \dfrac{3}{4})=\dfrac{11}{4}m/s$

And the distance at which the fish appears to approach is,
$42+\dfrac{\dfrac{24}{4}}{\dfrac{4}{3}}=60cm$

Therefore, image of the fish from the lens,
$V=\dfrac{-60\times 90}{-60+90}$ $=-180cm$

Therefore, the velocity of image with respect with respect to the lens,
${{V}_{1}}=(\dfrac{{{v}^{2}}}{{{u}^{2}}})\dfrac{du}{dt}$ $=\dfrac{-{{180}^{2}}}{-60}\times \dfrac{11}{4}=\dfrac{99}{4}m/s$

Velocity of image with respect to observer is,
${{V}_{1}}-2=\dfrac{99}{4}-2=\dfrac{91}{4}m/s=22.75cm/s$ (Upwards)

Therefore, $22.75cm/s$ is the velocity with which the fish appears to move to the observer.

The correct answer will be option B.

Note:
Now the question arises in our mind that what is focal length of a converging lens, there are two focal points for every lens, and the distance from the lens to the focal point is called focal length. And the focal length of a converging lens is always positive. As well, the focal length of a diverging lens is always negative.