Question

A stationary object explodes into masses ${{m}_{1}}$ and ${{m}_{2}}$. They move in opposite directions with velocities ${{v}_{1}}$ and ${{v}_{2}}$. The ratio of kinetic energy ${{E}_{1}}$ to kinetic energy ${{E}_{2}}$ is
$A.\quad \dfrac{{{m}_{2}}}{{{m}_{1}}}$
$B.\quad \dfrac{{{m}_{1}}}{{{m}_{2}}}$
$C.\quad \dfrac{2{{m}_{2}}}{{{m}_{1}}}$
$D.\quad \dfrac{2{{m}_{1}}}{{{m}_{2}}}$

Answer 1

Hint: To solve this problem, a diagram of the problem will be helpful. Along with that, the conservation of linear momentum, which is given by, ${{p}_{i}}={{p}_{f}}$. As per Newton’s second law, if no external force is acting, then momentum is conserved. The explosion occurs purely due to internal forces.

Step by step solution:
Let’s start by making a diagram of the problem.

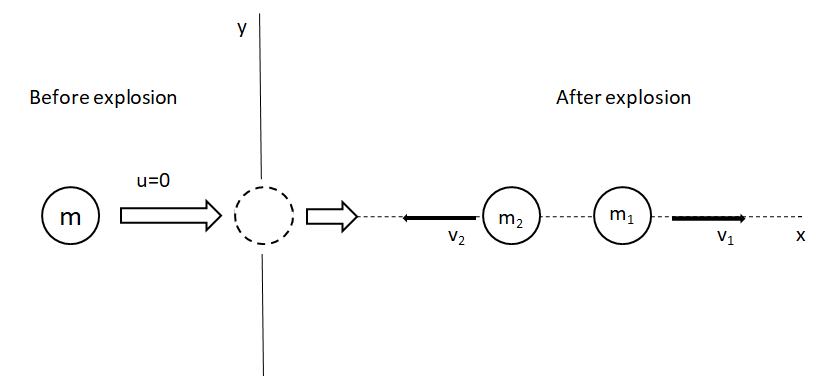
As per the problem, a stationary ball of mass (m) and initial velocity zero(u=0) after an explosion breaks into two masses ${{m}_{1}}$and ${{m}_{2}}$. These two masses move in opposite directions with velocities ${{v}_{1}}$ and ${{v}_{2}}$ respectively.

We will use the conservation of linear momentum now, given by, ${{p}_{i}}={{p}_{f}}$. The initial and final momenta will be equal. This means that, ${{p}_{i}}={{p}_{f}}\Rightarrow m(0)={{m}_{1}}(-{{v}_{1}})+{{m}_{2}}({{v}_{2}})\Rightarrow {{m}_{1}}({{v}_{1}})={{m}_{2}}({{v}_{2}})$. Hence, the ratio of the velocities will be equal to, $\dfrac{{{v}_{1}}}{{{v}_{2}}}=\dfrac{{{m}_{2}}}{{{m}_{1}}}$.
The final kinetic energy of the system after the explosion is the sum of the kinetic energies of the two bodies ${{E}_{1}}$ and ${{E}_{2}}$.

Finding the ratio of these two kinetic energies becomes, $\dfrac{{{E}_{1}}}{{{E}_{2}}}=\dfrac{\dfrac{1}{2}{{m}_{1}}{{({{v}_{1}})}^{2}}}{\dfrac{1}{2}{{m}_{2}}{{({{v}_{2}})}^{2}}}=\dfrac{{{m}_{1}}{{({{v}_{1}})}^{2}}}{{{m}_{2}}{{({{v}_{2}})}^{2}}}$. Now, substituting in the ratio of velocities that we found out earlier, the ratio of kinetic energies becomes, $\dfrac{{{E}_{1}}}{{{E}_{2}}}=(\dfrac{{{m}_{1}}}{{{m}_{2}}}){{(\dfrac{{{v}_{1}}}{{{v}_{2}}})}^{2}}=(\dfrac{{{m}_{1}}}{{{m}_{2}}}){{(\dfrac{{{m}_{2}}}{{{m}_{1}}})}^{2}}=\dfrac{{{m}_{2}}}{{{m}_{1}}}$. Hence it is equal to the ratio of the inverse of the masses.
So, the correct answer is option A.

Note:
Another way of solving this problem is by only using the momentums of the masses. From the conservation of momentum before and after the explosion become, ${{p}_{i}}={{p}_{f}}\Rightarrow m(0)={{p}_{1}}+{{p}_{2}}\Rightarrow {{p}_{1}}=-{{p}_{2}}$, where ${{p}_{1}}$and ${{p}_{2}}$are the momentum of the masses ${{m}_{1}}$and ${{m}_{2}}$respectively.

We also know that kinetic energy is given by $E=\dfrac{{{p}^{2}}}{2m}$. Again, we will remove the negative sign as it only states the direction, therefore $\dfrac{{{E}_{1}}}{{{E}_{2}}}=\dfrac{\dfrac{{{p}_{1}}^{2}}{2{{m}_{1}}}}{\dfrac{{{p}_{2}}^{2}}{2{{m}_{2}}}}=\dfrac{\dfrac{{{(-{{p}_{2}})}^{2}}}{{{m}_{1}}}}{\dfrac{{{p}_{2}}^{2}}{{{m}_{2}}}}=\dfrac{\dfrac{{{p}_{2}}^{2}}{{{m}_{1}}}}{\dfrac{{{p}_{2}}^{2}}{{{m}_{2}}}}=\dfrac{{{m}_{2}}}{{{m}_{1}}}$.