Question

A stationary man observes that the rain falling vertically downward. When he starts running with a velocity of 12km/h observes that the rain is falling at an angle 60° with the vertical. The actual velocity of rain with respect to running man is
A.$12\sqrt{3}km/h$
B. $12km/h$
C.$8\sqrt{3}km/h$
D.$10\sqrt{3}km/h$

Answer 1

In this question we are dealing with relative velocities, that is, velocity as observed by a stationary man is different from that observed by a running man. You could resolve the velocity of with respect to running man into its horizontal and vertical components. Taking the tangent will get you the velocity of rain with respect to the stationary observer. Then, you could substitute this to find the magnitude of velocity with respect to the running man.

Complete answer:
As per the observation of a stationary man the rain is falling vertically downward. Let the velocity of the rain with respect to stationary man be${{V}_{R}}$ .

This man now starts to run with a velocity V. Now, as per the observation of the running man the rain is falling at an angle 60° with the vertical.

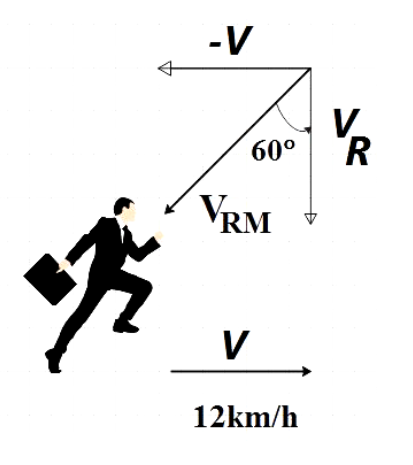
We are given the velocity V with which the man runs as,
$V=12km/h$ ………………………….. (1)
Now the velocity of rain with respect to the running man will be ‘${{V}_{RM}}$’.
Also, ${{V}_{RM}}$makes 60° with the vertical. If we resolve the vector ${{V}_{RM}}$ into its horizontal and vertical components, we could express the vector as the following.
${{V}_{RM}}=\left( -V \right)\widehat{i}+(-{{V}_{R}})\widehat{j}$ ………………………. (2)
We can find the velocity of rain with respect to the stationary man ${{V}_{R}}$ from,
$\tan 60{}^\circ =\dfrac{V}{{{V}_{R}}}$
$\sqrt{3}=\dfrac{12km/h}{{{V}_{R}}}$
${{V}_{R}}=\dfrac{12}{\sqrt{3}}=4\sqrt{3}km/h$ …………………………. (3)
Now we could find the magnitude of the velocity of rain with respect to the running man, that is, ${{V}_{RM}}$ by taking the magnitude of vectors on both LHS and RHS of equation (2). Doing so, we get,
$\left| {{V}_{RM}} \right|=\sqrt{{{\left( V \right)}^{2}}+{{\left( {{V}_{R}} \right)}^{2}}}$ ………………….. (4)
Substituting values for $V$ and ${{V}_{R}}$ from equations (1) and (3) in equation (4), we get,
$\left| {{V}_{RM}} \right|=\sqrt{{{\left( 12 \right)}^{2}}+{{\left( 4\sqrt{3} \right)}^{2}}}$
$\left| {{V}_{RM}} \right|=8\sqrt{3}km/h$ ……………….. (5)
Therefore, we get the velocity of the rain with respect to the running man as,
${{V}_{RM}}=8\sqrt{3}km/h$

Hence, the answer to the question is option C.

Note:
While dealing with problems related to relative motion between bodies, give importance to directions. You could draw a vector representation of the motion for better clarity of question. Doing so will also get you an idea on how to approach a given problem.