Question

A star of mass $M$ and radius $R$ is made up of gases. The average gravitational pressure compressing the star due to gravitational pull of the gases making up the star depends on $R$ as
(A) $1/{R^4}$
(B) $1/R$
(C) $1/{R^2}$
(D) $1/{R^6}$

Answer 1

Hint : To solve this question, we need to consider the free body diagram of an elementary cylinder at an arbitrary distance from the centre of the sphere. The cylinder will be acted upon by two forces, the gravitational force, and the force due to the pressure of the gases. Equating these two, we will get the required relation.

Formula used: The formula used to solve this question is given by
$g = \dfrac{{GM}}{{{R^2}}}$ , $g$ is the acceleration due to gravity on the surface of a sphere of mass $M$ and radius $R$ .

Complete step by step answer
The star has a radius of $R$ and mass $M$ . This means that the star is a sphere of radius $R$ and mass $M$ .
Let $\rho$ be the density of the gases, which make up this star. We know that the density is given by
$\rho = \dfrac{M}{V}$
As the star is a sphere, so its volume is $V = \dfrac{4}{3}\pi {R^3}$ . Substituting this above we get
$\rho = \dfrac{{3M}}{{4\pi {R^3}}}$ -----------(1)
We consider a hollow sphere inside the star, at a distance of $r$ from its center.

The depth of this sphere below the surface of the star, as can be observed from above, is
$d = R - r$ --------(2)
We know that the acceleration due to gravity decreases with the depth according to
$g\left( d \right) = g\left( {1 - \dfrac{d}{R}} \right)$
From equation (2)
$g\left( r \right) = g\left( {1 - \dfrac{{R - r}}{R}} \right)$
$\Rightarrow g\left( r \right) = g\left( {\dfrac{r}{R}} \right)$
Substituting $g = \dfrac{{GM}}{{{R^2}}}$ we get
$g\left( r \right) = \dfrac{{GMr}}{{{R^3}}}$ ---------(3)
Now we consider an elementary cylinder at a distance of $r$ from the center of the sphere, and of height $dr$ , as shown in the figure below.

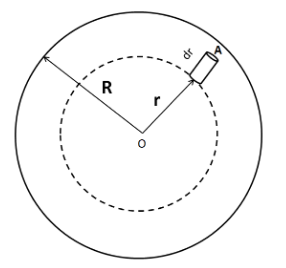
Let $A$ be its cross sectional area.
So the mass of the gases contained in the cylinder becomes
$dm = \rho Adr$ ---------(4)
The gravitational force on the cylinder, as we know, is given by
$d{F_g} = dm{\text{ }}g\left( r \right)$
From equation (3) we get
$d{F_g} = \dfrac{{GMr}}{{{R^3}}}dm$
From equation (4)
$d{F_g} = \dfrac{{GMr}}{{{R^3}}}\rho Adr$
$d{F_g} = \dfrac{{GM\rho A}}{{{R^3}}}rdr$ ---------(5)
We know that the pressure is given by
$P = \dfrac{F}{A}$
So the pressure $dP$ on the cylinder due to the gravitational pull of the gases is given by
$dP = \dfrac{{d{F_g}}}{A}$
From equation (5)
$dP = \dfrac{{GM\rho A}}{{A{R^3}}}rdr$
$\Rightarrow dP = \dfrac{{GM\rho }}{{{R^3}}}rdr$
So this is the pressure on the elementary cylinder, which is a part of the gases present. For the total pressure, we integrate both sides of (6) to get
$\int_0^P {dP} = \dfrac{{GM\rho }}{{{R^3}}}\int_0^R {rdr}$
$\left[ P \right]_0^P = \dfrac{{GM\rho }}{{{R^3}}}\left[ {\dfrac{{{r^2}}}{2}} \right]_0^R$
Substituting the limits we get
$P - 0 = \dfrac{{GM\rho }}{{{R^3}}}\left( {\dfrac{{{R^2}}}{2} - 0} \right)$
$\Rightarrow P = \dfrac{{GM\rho }}{{2R}}$
Substituting the density from (1) we finally get
$P = \dfrac{{GM}}{{2R}} \times \dfrac{{3M}}{{4\pi {R^3}}}$
$\Rightarrow P = \dfrac{{3G{M^2}}}{{8\pi {R^4}}}$
As $G$ and $M$ are constants, so we have
$P \propto \dfrac{1}{{{R^4}}}$
Hence, the correct answer is option A.

Note
We should not take the density of the star to be constant. As the sphere will shrink, its volume will decrease while the mass of the gases will remain the same. So the density will vary.