Question

A standing wave propagating with velocity $300m/s$ in an open pipe of length $4m$ has four nodes. The frequency of the wave is?
(A) $75Hz$
(B) $100Hz$
(C) $150Hz$
(D) $300Hz$
(E) $600Hz$

Answer 1

Hint : To solve this question, we need to find out the length of the pipe in terms of the wavelength with the help of the number of nodes given in the question. For this we have to draw the diagram of the nodes and antinodes in an open pipe and from that we can easily find out the relation. Then, we have to use the relation between the frequency and the wavelength to get the final answer.

Formula Used: The formula which is used to solve this question is given by
$\Rightarrow \lambda f = v$ , here $\lambda$ is the wavelength, $f$ is the frequency, and $v$ is the velocity of a wave.

Complete step by step answer
Let the frequency of the wave be $f$ .
According to the question, we have an open pipe in which a standing wave has four nodes. So, this situation can be represented by the below diagram.

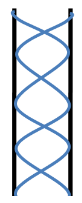
As we know that the distance between a node and an antinode is equal to one fourth of the wavelength of the light, so the total length of the pipe becomes
$\Rightarrow L = 8\left( {\dfrac{\lambda }{4}} \right)$
$\Rightarrow L = 2\lambda$
Dividing both the sides by $2$ , we get
$\Rightarrow \lambda = \dfrac{L}{2}$
According to the question, the length of the pipe is $4m$ . Therefore substituting $L = 4m$ above we get
$\Rightarrow \lambda = \dfrac{4}{2} = 2m$ (1)
So the wavelength of the wave is equal to $2m$ .
Now, we know that the frequency and the wavelength of a wave are related by the relation
$\Rightarrow \lambda f = v$
So the frequency of the wave is given by
$\Rightarrow f = \dfrac{v}{\lambda }$
According to the question, $v = 300m/s$ . Also, from (1) we have $\lambda = 2m$ . Substituting these above we get
$\Rightarrow f = \dfrac{{300}}{2}$
$\Rightarrow f = 150Hz$
Thus the frequency of the wave is equal to $150Hz$ .
Hence, the correct answer is option C.

Note
We need to be clear with the terminology of the organ pipes. An open organ pipe is a pipe which is closed at both the ends. While a closed organ pipe is closed only at one end. It must be noted that at least one end of the organ pipe must be open.