Question

A standing wave pattern is formed on a string. One of the waves is given by the equation $y_1 = a \cos \left(\omega t - kx + \frac{\pi}{3}\right)$. Then the equation of the other wave such that $x=0$ node is formed.

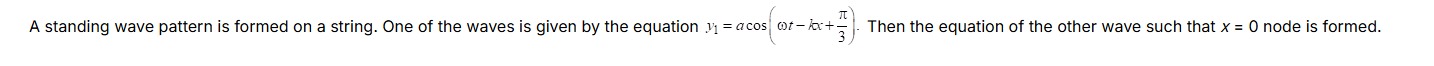
Answer 1

$y_2 = a \cos\left(\omega t + kx + \frac{4\pi}{3}\right)$

Answer 2

Let the second wave be

$$y_2 = a \cos(\omega t + kx + \phi)$$

For a node at $x = 0$, the total displacement must be zero for all $t$:

$$y(0, t) = y_1(0,t) + y_2(0,t) = a \cos(\omega t + \frac{\pi}{3}) + a \cos(\omega t + \phi) = 0\quad \forall\, t$$

This requires:

$$\cos(\omega t + \phi) = -\cos(\omega t + \frac{\pi}{3})$$

Since we know $-\cos(\theta) = \cos(\theta \pm \pi)$, we choose:

$$\phi = \frac{\pi}{3} + \pi = \frac{4\pi}{3}$$

Thus, the equation for the second wave becomes:

$$y_2 = a \cos\left(\omega t + kx + \frac{4\pi}{3}\right)$$