Question

A standing man, observes rain falling with velocity of 20$m{{s}^{-1}}$ at an angle of ${{30}^{0}}$ with the vertical. Now, if he further increases his speed, rain again appears to fall at ${{30}^{0}}$ with the vertical. Find his new velocity.

& \text{A) 10}\sqrt{3}m{{s}^{-1}} \\\ & \text{B) 20m}{{\text{s}}^{-1}} \\\ & \text{C) 40}\sqrt{3}m{{s}^{-1}} \\\ & \text{D) 10m}{{\text{s}}^{-1}} \\\ \end{aligned}$$

Answer 1

We need to find the relation between the velocity of the rain, it’s angle with the vertical and the velocity of the man to solve the problem. We can easily find the solution by using the trigonometric properties in the current situation.

Complete step by step solution:
We are given the situation in which the rain is falling to the ground making an angle of ${{30}^{0}}$ with the vertical.

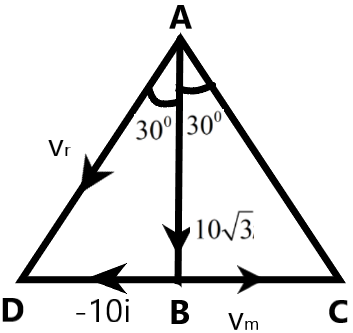
It is given that the rain falls with a velocity of 20 $m{{s}^{-1}}$along the direction of the rainfall. We can resolve the direction of velocity of the rain using the trigonometric relations.

& v=20m{{s}^{-1}} \\\ & \Rightarrow v\cos \theta =20\cos {{30}^{0}} \\\ & \Rightarrow v\cos \theta =10m{{s}^{-1}} \\\ & \Rightarrow v\sin \theta =20\sin {{30}^{0}} \\\ & \Rightarrow v\sin \theta =10\sqrt{3}m{{s}^{-1}} \\\ & \therefore \overrightarrow{v}=(-10\widehat{i}-10\sqrt{3}\widehat{j})m{{s}^{-1}} \\\ \end{aligned}$$ Now, we are given that the man experiences the rain to be $${{30}^{0}}$$ with the man when he moves with a certain velocity. So, he has to be moving in a direction opposite to the rain for this to be possible. We know that the velocity of the man is only along the horizontal component. We can find the relative velocity of the rain with respect to the man by finding the difference between their velocities as – $$\begin{aligned} & \overrightarrow{{{v}_{rm}}}=\overrightarrow{{{v}_{r}}}-\overrightarrow{{{v}_{m}}} \\\ & \Rightarrow \overrightarrow{{{v}_{rm}}}=(-10\widehat{i}-10\sqrt{3}\widehat{j})-(-{{v}_{m}}i) \\\ & \therefore \overrightarrow{{{v}_{rm}}}=(-10+{{v}_{m}})\widehat{i}-10\sqrt{3}\widehat{j} \\\ \end{aligned}$$ The angle with the vertical of the rain is $${{30}^{0}}$$. We can use the tangent of the angle to find the velocity of the man as – $$\begin{aligned} & \text{In }\Delta \text{ABC,} \\\ & \tan {{30}^{0}}=\dfrac{10-{{v}_{m}}}{-10\sqrt{3}} \\\ & \Rightarrow \dfrac{1}{\sqrt{3}}=\dfrac{10-{{v}_{m}}}{-10\sqrt{3}} \\\ & \therefore {{v}_{m}}=20m{{s}^{-1}} \\\ \end{aligned}$$ The velocity of the man should be 20 $$m{{s}^{-1}}$$ along the positive x-axis to get the required solution. **The correct answer is option B.** **Note:** The velocity of the rain, the velocity of the moving person and the angle of the rain with the vertical is used to calculate the angle at which the shades for rain shelters and umbrellas can be arranged. We can use this information in our daily life.