Question
Question: A staircase contains three steps each 10cm high and 20cm wide. What should be the minimum horizontal...
A staircase contains three steps each 10cm high and 20cm wide. What should be the minimum horizontal velocity of a ball rolling off the uppermost plane so as to hit directly the lowest plane?
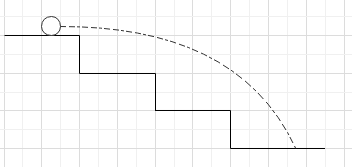
Solution
Here in the given situation we have to find the minimum velocity required for the ball to land on the lowest plane directly from the uppermost plane or stair. The ball will have a trajectory while having the motion. Considering the formula for the trajectory and redrawing the diagram we can find the minimum horizontal velocity of the ball.
Formula used:
y=xtanθ−2u2cos2θgx2
Complete step-by-step solution:
From the data given in the question, we know the width and height of each stair. Now for minimum velocity, the ball just has to cover the distance of two stairs. As when it reaches the end of the second stair it will ultimately land on the last one. Hence the vertical displacement should be 20 cm and horizontal displacement should be 40cm.
Let us redraw the diagram for better understanding,
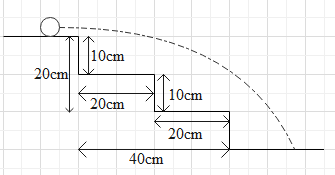
The trajectory for the vertical displacement is given as
y=xtanθ−2u2cos2θgx2
Where x is the horizontal displacement, g is the acceleration due to gravity, u is the initial velocity and θ is the angle of elevation with respect to horizontal displacement.
Now, according to the question, the vertical displacement y and horizontal displacement x is given. g is the constant value whereas the angle of elevation will be zero as there is downward motion instead of upward motion so there won’t be any elevation and the motion is also in the horizontal direction.
As discussed earlier, for minimum velocity the vertical displacement should be 20cm (height 10cm each) and the horizontal displacement should be 40cm (two stairs of width 20cm each). Value of g is 9m/s2and θ=0. The value of x in meters will be 0.4m and the value of y in meters will be 0.2m.
Substituting the value in the above equation we get
