Question

A staircase contains three steps each $10cm$ high and $20cm$ wide as shown in the figure. Calculate the minimum horizontal velocity of a ball which is rolling down the uppermost plane in order to hit directly the lowest plane?
$\begin{aligned} & A.0.5m{{s}^{-1}} \\\ & B.1m{{s}^{-1}} \\\ & C.2m{{s}^{-1}} \\\ & D.4m{{s}^{-1}} \\\ \end{aligned}$

Answer 1

First of all find the time taken for the travel of the horizontal range. This can be found by taking the ratio of the distance travelled and the velocity of the ball. And also the displacement of the ball should also be calculated. Newton’s second law can be used to find the time taken. Using all these the horizontal velocity of the ball can be calculated.

Complete step-by-step answer:

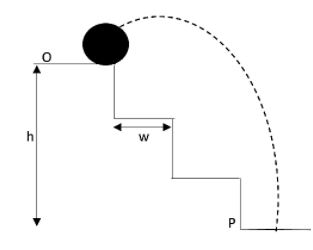
Let us assume that the height of the stair is $h$, width of each step is given as $w$, uppermost plane is indicated as $O$ and the lowermost plane will be represented as $A$.
Let us assume that the ball rolls from the utmost plane $O$ with horizontal velocity $v$ here the vertical velocity in the y direction will be zero.
That is,
$X=vt$
Equation can be rearranged as,
$t=\dfrac{X}{v}$………. (1)
The horizontal range of the ball will be lying between $2w$ and $3w$.
Therefore the horizontal range $X$ of the ball will be greater than $2w$.
That is,
$X\ge 2w$
It is mentioned in the question that,

& h=10cm=0.1m \\\ & w=20cm=0.2m \\\ \end{aligned}$$ Substituting this in the above inequality will give, $$\begin{aligned} & X\ge 2\times 0.2 \\\ & \Rightarrow X\ge 0.4m \\\ \end{aligned}$$ That is the ball travels from uppermost plane to the lowermost plane by a displacement, $$s=2h$$ According to the newton’s second equation of motion, $$s=ut+\left( \dfrac{1}{2}g{{t}^{2}} \right)$$ The initial velocity will be zero in vertical motion, $$u=0$$ Substituting all other values in it will give, $$2h=0+\left( \dfrac{1}{2}g{{t}^{2}} \right)$$ Rearranging the equation will give, $$t=\sqrt{\dfrac{4h}{g}}$$……….. (2) From the equations (1) and (2), we can write that, $$\dfrac{X}{v}=\sqrt{\dfrac{4h}{g}}$$ That is, $$X=v\sqrt{\dfrac{4h}{g}}$$ We know that, $$X\ge 0.4m$$ That is, $$v\sqrt{\dfrac{4h}{g}}\ge 0.4m$$ Substituting the values in the equation will give, $$\begin{aligned} & v\sqrt{\dfrac{4\times 0.1}{10}}\ge 0.4m \\\ & \Rightarrow 0.2v\ge 0.40 \\\ \end{aligned}$$ From this we can say that, $$v\ge 2m{{s}^{-1}}$$ **So, the correct answer is “Option C”.** **Note:** Horizontal range is defined as the distance of the body moving along the horizontal plane. The velocity is defined as the change in position of a particle as per the variation in time. The velocity is a vector quantity. That is it depends on both magnitude as well as direction.