Question
Question: A staircase contains three steps each \(10cm\) high and \(20cm\) wide. What should be the minimum ho...
A staircase contains three steps each 10cm high and 20cm wide. What should be the minimum horizontal velocity of a ball rolling off the uppermost plane so as it hits directly the lowest plane?
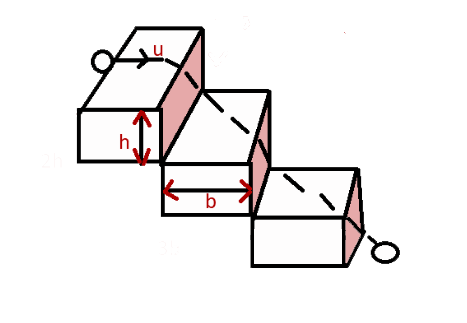
Solution
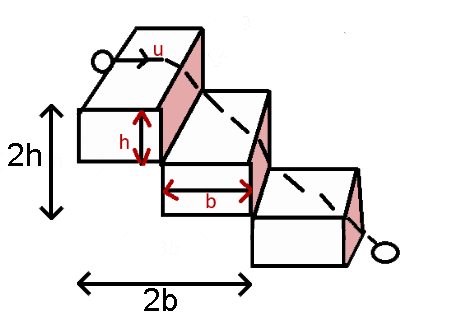
The vertical and horizontal distance covered by the body will be 2h and 2b respectively. You can start by using the second equation of motion, i.e. h=ut+21at2 for the vertical motion of the ball and calculate the value of t . Then put this value of t in the equation for the speed of the horizontal motion of the body, i.e. s=td .
Complete answer:
In the problem given to us
Height of each step of the staircase, h=10cm
Width of each step of the staircase, b=20cm
Let the initial speed of the ball and time taken by the ball to hit the lowest plane be u and t respectively.
The total horizontal distance that the ball has to cover is equal to the width of two steps of the staircase combined =2b=2×20=40cm=0.4m
We know that the equation for speed is
s=td
s= Speed of the ball
d= The horizontal distance that the ball covers
t= The time taken by the ball to cover the distance.
This equation can be used to calculate the horizontal speed of the equation as follows
u=t2b
u=t0.4
t=u0.4 (Equation 1)
Now it becomes clear that to calculate the horizontal speed of the ball we have to calculate the time taken by the ball to hit the lowest stair.
Total vertical distance by the ball covers
We know that the second equation of motion is
h=ut+21at2
Here, h= Height
u= The initial speed of the ball
t= Time
a=9.8m/s2= The acceleration due to gravity
So, for the vertical motion of the ball
0.2=0×t+21×9.8×t2
t2=9.80.4
t2=0.04
t=0.2sec
Now, substituting the value of t in equation 1 we get
0.2=u0.4
u=0.20.4
u=2m/s
Hence, the ball must have a minimum horizontal velocity of 2m/s to hit the lowest step of the staircase without hitting the steps in the middle.
Note:
In the problem given to us we had to calculate the minimum horizontal velocity of the ball to hit the lowest step of the staircase without hitting the steps in the middle. If you had to calculate the maximum horizontal velocity the steps of calculation would remain the same but you would take horizontal as 3b instead of 2b.
