Question

A squirrel runs between two adjacent corners of a prayer hall along the floor. The velocity of the squirrel is uniform and is $1{\text{m}}{{\text{s}}^{ - 1}}$ . The roof of the hall has a gentle slope of $\dfrac{1}{{\sqrt 3 }}$ and is a plane mirror. Find the velocity of the squirrel’s image in the mirror.
A) The same as that of the squirrel.
B) Has a value $\dfrac{1}{{\sqrt 3 }}{\text{m}}{{\text{s}}^{ - 1}}$ .
C) Has a value $\dfrac{2}{{\sqrt 3 }}{\text{m}}{{\text{s}}^{ - 1}}$ .
D) Has a value $\left( {1 + \dfrac{1}{{\sqrt 3 }}} \right){\text{m}}{{\text{s}}^{ - 1}}$ .

Answer 1

The image formed on a plane mirror is known to be virtual, erect, and laterally inverted. So the image formed of the squirrel on the slightly slanted mirror will have the same properties as that of the image formed if the mirror was not slanted. But the position of the image of the squirrel in the plane mirror would be different.

Formulas used:
The time taken to cover a distance is given by, $t = \dfrac{s}{v}$ where $s$ is the distance and $v$ is the velocity with which it is covered.
The velocity of a body is given by, $v = \dfrac{s}{t}$ where $s$ is the distance and $t$ time taken to cover the distance.

Complete step by step answer:
Step 1: Describing the motion of the image of the squirrel relative to that of the squirrel on the floor.
The slope of the mirror is given to be $\dfrac{1}{{\sqrt 3 }}$ i.e., $\tan \theta = \dfrac{1}{{\sqrt 3 }}$.
$\Rightarrow \theta = {\tan ^{ - 1}}\left( {\dfrac{1}{{\sqrt 3 }}} \right) = 30^\circ$.
So the mirror is inclined at an angle of $\theta = 30^\circ$ with the floor.

We know that the image formed on the plane mirror is virtual, erect, and laterally inverted. The squirrel will thus reach the corners of the hall at the same instants but due to the slight inclination of the mirror, the distance travelled by the squirrel and its image will be different for the same time $t$.
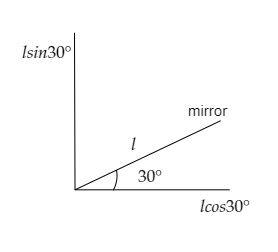
Let $l$ be the length of the mirror.
The velocity of the squirrel is given to be ${v_s} = 1{\text{m}}{{\text{s}}^{ - 1}}$ .
Let ${v_s}^\prime$ be the velocity of the image of the squirrel.
The length of the mirror can be resolved into its x-component $l\cos 30^\circ = \dfrac{{\sqrt 3 l}}{2}$ and y-component $l\sin 30^\circ = \dfrac{l}{2}$ as shown in the figure below.

Step 2: Expressing the time taken by the squirrel to reach the adjacent corner.
The time taken by the squirrel to cover the x-component distance of the length of the mirror can be expressed as $t = \dfrac{{l\cos 30^\circ }}{{{v_s}}}$ ------- (1)
Substituting for $l\cos 30^\circ = \dfrac{{\sqrt 3 l}}{2}$ and ${v_s} = 1{\text{m}}{{\text{s}}^{ - 1}}$ in equation (1) we get, $t = \dfrac{{\sqrt 3 l}}{2}{\text{s}}$ .
Thus the time taken by the squirrel to reach the adjacent corner is $t = \dfrac{{\sqrt 3 l}}{2}{\text{s}}$ .
Step 3: Expressing the velocity of the image of the squirrel.
In $t = \dfrac{{\sqrt 3 l}}{2}{\text{s}}$ , the image of the squirrel travels the length of the mirror.
The velocity of the image of the squirrel can be expressed as ${v_s}^\prime = \dfrac{l}{t}$ --------- (2)
Substituting for $t = \dfrac{{\sqrt 3 l}}{2}{\text{s}}$ in equation (2) we get, ${v_s}^\prime = \dfrac{{2l}}{{l\sqrt 3 }} = \dfrac{2}{{\sqrt 3 }}{\text{m}}{{\text{s}}^{ - 1}}$
Thus the velocity of the image of the squirrel will be ${v_s}^\prime = \dfrac{2}{{\sqrt 3 }}{\text{m}}{{\text{s}}^{ - 1}}$ .

Therefore, the correct option is C.

Note:
In the time $t = \dfrac{{\sqrt 3 l}}{2}{\text{s}}$, the distance covered by the image of the squirrel will be equal to the length of the plane mirror while the distance covered by the squirrel on the floor as it runs between adjacent corners will be equal to the x-component of the length of the plane mirror. The slope of a line is often referred to as $\tan \theta$ where $\theta$ is the angle at which the line is slanted.