Question
Question: A square wire frame of side \( a \) is placed \( b \) away from a long straight conductor carrying c...
A square wire frame of side a is placed b away from a long straight conductor carrying current I . The frame has resistance R and self-inductance L . The frame is rotated by 180∘ about OO′ as shown in figure. Find the electric charge flown through the frame.
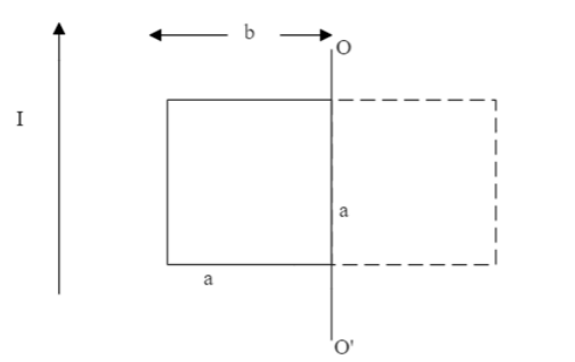
(A) 2πRb2μ0ia2
(B) 2πRμ0ilogeb−ab+a
(C) 2πRμ0ialogeb−ab+a
(D) None of these
Solution
We know that the faraday's law stated that a changing magnetic field produces an electric field. So charges that are free to move will cause an EMF and a current. Thus the magnetic statement of Faraday’s Law is that EMF induced in a loop is proportional to rate of change in flux.
E=iR=ΔtΔϕ
We also know that the current in a conductor is nothing but, charge flowing in it per unit time i=tq
We also know that, ϕ=∫B.dA .
Formulas used: We will be using the formula E=iR=ΔtΔϕ where E is the EMF induced by current i , flowing through a conductor with resistance R and Δϕ is the change in flux of the body, while Δt is the change in time intervals. We will also be using, ϕ=∫B.dA where B is the magnetic field intensity produced due to the flux and dA is the change in area.
Complete Step by Step Solution
We know that by faraday’s Laws of electromagnetism, E=iR=ΔtΔϕ we also know that q=it , Thus the charge induced on a body can be given by, ΔtQindR=ΔtΔϕ .
⇒Qind=RΔϕ .
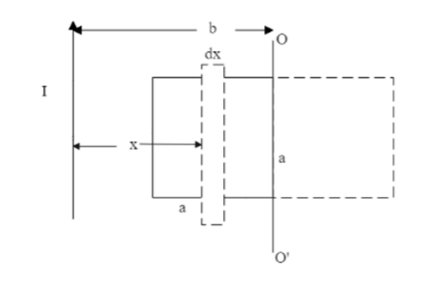
Consider a small strip of width dx at the distance of x from the current carrying wire.So let us find the change in flux by finding the final flux and initial flux.
dϕ=B.dA
Integrating the expression to find the initial and final fluxes of the thin strip
∫dϕ=∫B.dA
We know that ∫dϕ=ϕ and B=2πxμ0I . Also the are of the strip will be A=a×dx .
Substituting the values be get,
ϕ=∫2πxμ0I×adx
The limits can be specified to be, (b−a) to b .
ϕ=2πμ0Ia∫b−abxdx=2πμ0Ia[logeb−loge(b−a)]
⇒ϕ=2πμ0Ialoge(b−ab)
Now, consider the final position to find flux for,
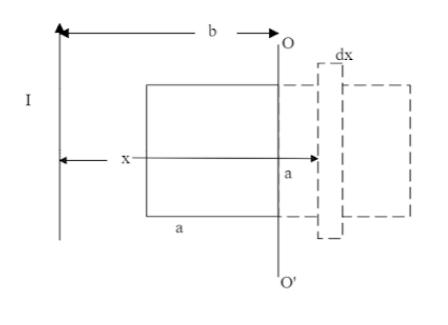
Finding flux using integration,
ϕ=∫2πxμ0I×adx
but the limits will be b to b+a .
ϕ=2πμ0Ia∫bb+axdx=2πμ0Ia[loge(b+a)−loge(b)]
⇒ϕ=2πμ0Ialoge(bb+a)
Now we have both the initial and final flux let us find the differences between them, Δϕ=ϕf−(−ϕi)=2πμ0Ialoge(bb+a)−2πμ0Ialoge(b−ab)
Since ϕ=B.dAcosθ and here θ=180∘
Δϕ=2πμ0Ialoge[(bb+a)×(b−ab)]
⇒Δϕ=2πμ0Ialoge(b−ab+a)
Since we know that Qind=RΔϕ ,
Q=2πRμ0Ialoge(b−ab+a)
Hence the correct answer is option C.
Note
The problem can also be solved without breaking the limits and taking , solving for, ϕ=2πμ0Ia∫b−ab+axdx=2πμ0Ia[loge(b+a)−loge(b−a)]
⇒ϕ=2πμ0Ia[loge(b+a)−loge(b−a)]=2πμ0Ialoge(b−ab+a)
Thus Qind will be, Q=2πRμ0Ialoge[b−ab+a] .
