Question

A square whose side is $2$ meters has its corners cut away so as to form an octagon with all sides equal. Then, the length of each side of the octagon in meters is:
A) $\dfrac{{\sqrt 2 }}{{\sqrt {2 + 1} }}$
B) $\dfrac{2}{{\sqrt {2 + 1} }}$
C) $\dfrac{2}{{\sqrt {2 - 1} }}$
D) $\dfrac{{\sqrt 2 }}{{\sqrt {2 - 1} }}$

Answer 1

In this solution, first, we have to assume a square ABCD of side’s $2$meters and mark all the sides as shown in the diagram. Now we use Pythagoras theorem in the triangle ${\rm{\Delta ALE}}$ to find the side of the triangle. Once we get the sides, we use that value to find the side of the octagon.

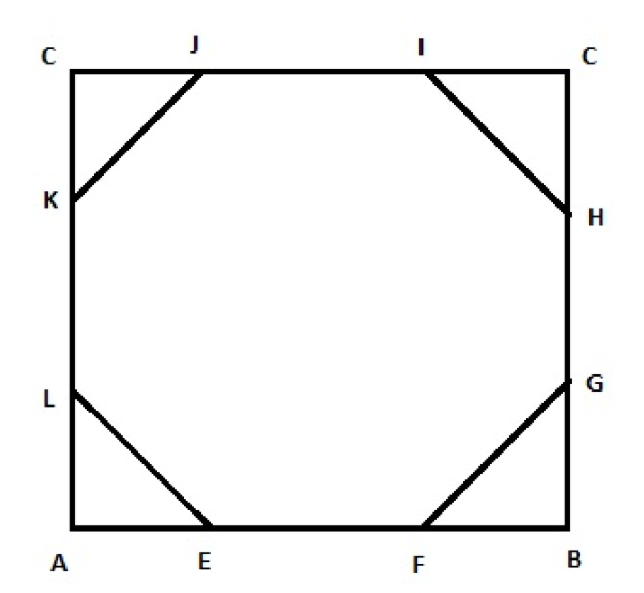
Complete step-by-step answer:
Let us consider ABCD to be a square of side $2$ meters. We form a regular octagon by cutting all four corners.
Let,
EF = FG = GH = HI = IJ = JK = KL = LE = $x$
By symmetry,
AE = AL = BG = BF = CH = CI = DJ = DK = ${\rm{a}}$
Using,
Pythagoras theorem in ${\rm{\Delta ALE}}$, we get
$\begin{array}{c}{\rm{L}}{{\rm{E}}^{\rm{2}}} = {\rm{A}}{{\rm{L}}^{\rm{2}}}{\rm{ + A}}{{\rm{E}}^{\rm{2}}}\\\\{{\rm{x}}^{\rm{2}}} = {{\rm{a}}^{\rm{2}}}{\rm{ + }}{{\rm{a}}^{\rm{2}}}\\\ = {\rm{2a}}\end{array}$

Take the square root on both sides.
$\Rightarrow {\rm{x = }}\sqrt {{\rm{2a}}}$

And,
AB $=$ AE $+$EF$+$FB
$\begin{array}{l} \Rightarrow {\rm{2}} = {\rm{a + x + a}}\\\ \Rightarrow {\rm{2}} = {\rm{2a + x}}\\\ \Rightarrow {\rm{2a + x}} = {\rm{2}}\end{array}$
Now,
Putting the value of x in the above equation, we get
$\begin{array}{l} \Rightarrow {\rm{2a + }}\sqrt {{\rm{2a}}} = {\rm{2}}\\\ \Rightarrow {\rm{a}}\left( {{\rm{2 + }}\sqrt {\rm{2}} } \right) = {\rm{2}}\\\ \Rightarrow {\rm{a}}\sqrt {\rm{2}} \left( {\sqrt {{\rm{2 + 1}}} } \right) = {\rm{2}}\\\ \Rightarrow {\rm{a}} = \dfrac{2}{{\sqrt {{\rm{2 + 1}}} }}\end{array}$
Thus, the length of each side of the octagon is $\dfrac{2}{{\sqrt {\rm{2}} {\rm{ + 1}}}}\,{\rm{m}}$.

Hence, the correct option is B.

Note: An octagon is a geometric shape having eight sides and eight angles, and a square is a regular quadrilateral, meaning it has four equal sides and four equal corners. It can also be defined as a rectangle, where the length of two adjacent sides is equal. The ABCD will be denoted as a square with vertices. We need to cut down all four corners of a square to create an octagon from a square.