Question
Question: A square plate of mass m and length a is free to rotate about the axis \(X{{X}_{C}}\) shown in the f...
A square plate of mass m and length a is free to rotate about the axis XXC shown in the figure at a distance a/4 from the edge. If is released from the horizontal position shown in the figure, find the angular speed attained by the plate when it passes through the vertical position
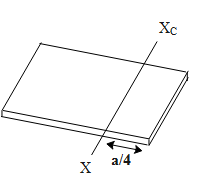
a)7a3gb)7a12gc)5a24gd)7a24g
Solution
In the above figure we can see that the sheet is free to move about the axis when released. Hence when released all the potential energy of the centre of mass will get converted to the kinetic energy when the centre of mass reaches the vertical position. Hence we will equate the potential energy of the centre of mass to the rotational kinetic energy and obtain the angular speed.
Formula used: K.E(rotational)=21Iω2
I(axis of rotation)=12Ma2
I(centre of mass)=I(axis of rotation)−Md2
Potential energy at height (h)=mgh
Complete step by step answer:
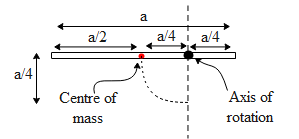
In the above figure we can see the transverse section of the sheet. When the sheet is released its centre of mass comes down to a height of a/4. Hence all its potential energy gets converted to the rotational kinetic energy. Let us say the sheet rotates along the axes at an angular speed ωand the moment of inertia along the axes of rotation be I. Hence its rotational kinetic energy is given by,
K.E(rotational)=21Iω2. The moment of inertia along the centre of mass of a sheet is given by 12Ma2 where M is the mass of the sheet and a is the length of the sheet along which the sheet is rotated. In the above figure we can see that the axis of rotation of the above sheet is at a distance of a/4 from the centre of mass. Hence using the parallel axis theorem, the moment of inertia along the axis of rotation is equal to,
I(centre of mass)=I(axis of rotation)−Md2 where M is the mass of the sheet and d is the distance between the centre of mass and the axis of rotation. We know that this distance is equal to a/4. Hence the moment of inertia along the axis of rotation is,
I(centre of mass)=I(axis of rotation)−Md2⇒12Ma2=I(axis of rotation)−M(a/4)2⇒I(axis of rotation)=12Ma2+16Ma2⇒I(axis of rotation)=12Ma2+16Ma2⇒I(axis of rotation)=12×1628Ma2⇒I(axis of rotation)=487Ma2
The loss of potential energy of the sheet is given byMg(a/4) where M is the mass of the sheet, g is the acceleration due to gravity and a/4 is the distance by which the distance from the ground of the centre has decreased. Since this energy is equal to the rotational kinetic energy we can write,
21Iω2=Mg(a/4)⇒21(487Ma2)ω2=4Mga⇒(247a)ω2=g⇒ω2=7a24g⇒ω=7a24g
So, the correct answer is “Option D”.
Note: All the net effects on the sheet can be considered equivalent to the effect on the centre of mass of the sheet. Hence we have considered. It is to be noted that every point on the sheet will have the same angular velocity. But the linear velocity of the sheet at every point will be different i.e. the points closer to the line passing through the axis of rotation will possess greater velocity than those at the extreme.
