Question

A square plate and a circular plate made up of same material are placed touching each other on horizontal table. If the side length of square plate is equal to diameter of the circular plate then the centre of mass of the combination will be

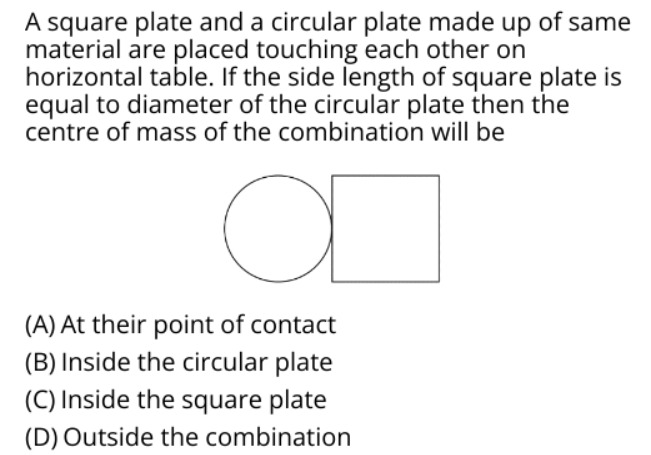
• A. At their point of contact
• B. Inside the circular plate
• C. Inside the square plate
• D. Outside the combination

Answer 1

Answer: (C)

Inside the square plate

Answer 2

Let the radius of the circular plate be $r$. Its diameter is $2r$. The side length of the square plate is $s = 2r$. Since the material is the same, the surface density $\sigma$ is constant. Mass of circular plate: $m_c = \sigma \times (\pi r^2)$. Its center of mass is at its geometric center. Mass of square plate: $m_s = \sigma \times (2r)^2 = \sigma \times 4r^2$. Its center of mass is at its geometric center.

Since $4 > \pi$, the mass of the square plate ($m_s$) is greater than the mass of the circular plate ($m_c$). Let the point of contact be the origin (0,0). Let the circular plate be centered at $(-r, 0)$ and the square plate be centered at $(r, 0)$. The x-coordinate of the center of mass of the combination is: $X_{CM} = \frac{m_c(-r) + m_s(r)}{m_c + m_s} = \frac{\sigma \pi r^2 (-r) + \sigma 4r^2 (r)}{\sigma \pi r^2 + \sigma 4r^2}$ $X_{CM} = \frac{-\sigma \pi r^3 + \sigma 4r^3}{\sigma r^2 (\pi + 4)} = \frac{\sigma r^3 (4 - \pi)}{\sigma r^2 (\pi + 4)} = r \frac{4 - \pi}{\pi + 4}$

Since $4 > \pi$, $4 - \pi > 0$, so $X_{CM} > 0$. This means the center of mass is to the right of the point of contact. Since $4 - \pi < \pi + 4$, $\frac{4 - \pi}{\pi + 4} < 1$, so $X_{CM} < r$. Thus, $0 < X_{CM} < r$. The square plate extends from $x=0$ to $x=2r$. Since $X_{CM}$ is between $0$ and $r$, it lies within the square plate.