Question

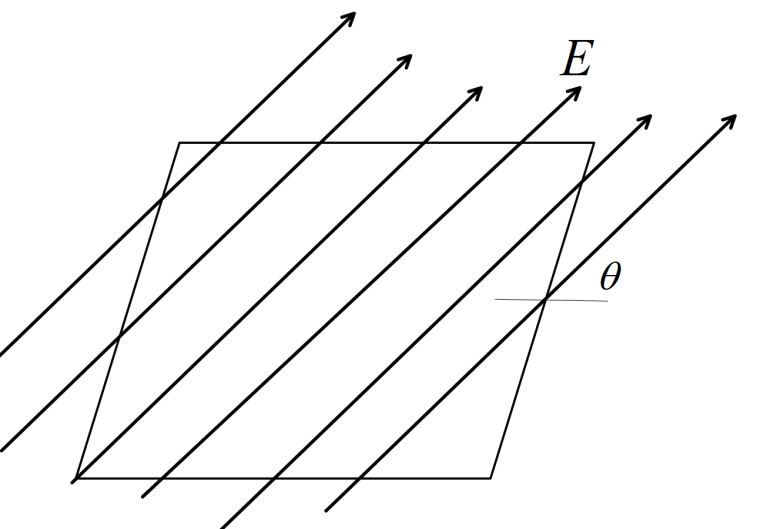
A square of side $L$ meter in the plane of the paper is placed in a uniform electric field $E(volt/m)$ acting along the same plane at an angle with the horizontal side of the square as shown in the figure. Find The electric flux linked to the surface, in units of $volt \cdot m$ .

Answer 1

Find the total flux linked with the surface from the definition of electric flux linked to a surface. The electric flux linked to a surface is given by $\phi = \oint\limits_s {\vec E} .d\vec S$ , $\vec E$ is the electric field , $S$ is the closed surface placed in the electric field. Direction of $S$ is always normal to it.

Complete answer:
We know that the, electric flux passing through a surface $S$ is given by $\phi = \oint\limits_s {\vec E} .d\vec S$ where, $\phi$ is the flux linked with the surface, $d\vec S$ is the elementary surface area , direction of which is along the normal.
Here, we have given a square of side $L$ $m$ placed in the plane of paper. So, the direction of the surface is towards the paper. if we take direction out of the paper as the $Z$ direction then the elementary surface vector becomes, $d\vec S = dS\hat k$ .

Also here we have , the uniform electric field is on the plane of paper making an angle $\theta$ with the horizontal side of the square. Hence, the uniform electric vector $\vec E$ can be written as, $\vec E = E\cos \theta \hat i + E\sin \theta \hat j$ . Since, $\vec E$ can be divided into two components lying in the $XY$ plane . (See the figure)
Now, let’s find the flux of the electric vector using the formula $\phi = \oint\limits_s {\vec E} .d\vec S$ .
Putting the value of $\vec E$ and $d\vec S = dS\hat k$ that becomes,
$\phi = \oint\limits_s {(E\cos \theta \hat i + E\sin \theta \hat j)} .dS\hat k$
Which is on simplifying,
$\Rightarrow \phi = \oint\limits_s {E\cos \theta \hat i.dS\hat k + E\sin \theta \hat j.dS\hat k}$
Now we know, dot product of the mutually orthogonal unit vectors gives zero which is, $\hat i.\hat j = \hat j.\hat k = \hat k.\hat i = 0$
Therefore, the integration of becomes,
$\Rightarrow \phi = \oint\limits_s {E\cos \theta dS\hat i.\hat k + E\sin \theta dS\hat j.\hat k}$
Putting the values we get,
$\Rightarrow \phi = \oint\limits_s {E\cos \theta dS.0 + E\sin \theta dS.0}$
$\Rightarrow \phi = 0 + 0 = 0$
$\therefore \phi = 0$
Therefore, the flux linked with the square $L$ of side, kept in an electric field $E(volt/m)$ making an angle $\theta$ with the horizontal is, $0V.m$ .

Note:
If the square is placed perpendicular to the Electric field or making an angle with the plane of the electric field then only some flux will be linked with the surface except that the total flux is zero. This is true for any surface placed in an electric field or in a magnetic field (magnetic flux).