Solveeit Logo
Login

Question

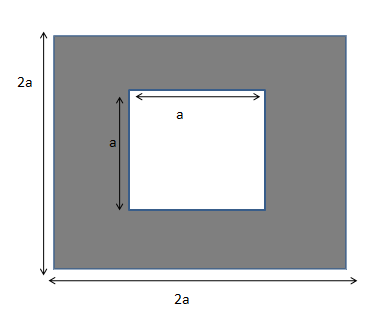
Question: A square of side \[\;a\] is cut from a square of side ‘\[2a\] ’ as shown in fig. Mass of this square...

A square of side   a\;a is cut from a square of side ‘2a2a ’ as shown in fig. Mass of this square with a hole isMM . Then its moment of inertia about an axis passing through its CM and perpendicular to its plane will be?

Explanation

Solution

Initially we find the mass of the remaining part. To solve this question we need to find out the formula for the moment of inertia for the square lamina whose axis is passing through the center of mass or the center of the square and is perpendicular to the plane. So finally after simplifying by applying the moment of inertia to the square that is taken, subtracting both, we get the required relation.

Complete step by step solution:
By perpendicular axis theorem we can find the moment of inertia of the plate about the axis passing through the center and parallel to the z-axis which is perpendicular to the plate). We know, Perpendicular axis theorem states that,
I(z)=I(x)+I(y)I\left( z \right) = I\left( x \right) + I(y)
Thus, the Moment of Inertia of the square plate about the axis passing through the center and perpendicular to it will be, I(z)=(ma2)6I(z) = \dfrac{{(m{a^2})}}{6}
Mass of remaining part =M3a2×a2=M3 = \dfrac{M}{{3{a^2}}} \times {a^2} = \dfrac{M}{3}
Mass per unit area =M4a2−a2=M3a2 = \dfrac{M}{{4{a^2} - {a^2}}} = \dfrac{M}{{3{a^2}}}
Mass of square without hole =M3a2×4a2=4M3 = \dfrac{M}{{3{a^2}}} \times 4{a^2} = \dfrac{{4M}}{3}
Mass of part is taken out = M3a2×a2=M3 = \,\dfrac{M}{{3{a^2}}} \times {a^2} = \dfrac{M}{3}
Moment of Inertia of the total without hole about the center of mass or the center of the square can be given as 16×4M3×2a2=16Ma218\dfrac{1}{6} \times \dfrac{{4M}}{3} \times 2{a^2} = \dfrac{{16M{a^2}}}{{18}}
Moment of Inertia of the square part taken out about center of mass:
Ma218\dfrac{{M{a^2}}}{{18}}
Moment of Inertia of remaining part
=16Ma218−Ma218= \dfrac{{16M{a^2}}}{{18}} - \dfrac{{M{a^2}}}{{18}}
=5Ma26= \dfrac{{5M{a^2}}}{6}
Therefore the Correct option is option D.

Note: Moment of inertia remains unchanged if the mass, distance from the axis, and the distribution of mass about that axis remain the same. Moment of inertia of about an axis parallel to a side and bisecting the other side at the midpoint is ma212\dfrac{{m{a^2}}}{{12}}. In the same manner, the other axis perpendicular to this is also the same because the square is symmetric.