Question

A square of side 3 mm is placed at a distance of 25 cm from a concave mirror of focal length 10 cm. The centre of the square is at the axis of the mirror and the plane is normal to the axis. The area enclosed by image of square is
A. 4 $mm^2$
B. 6 $mm^2$
C. 18 $mm^2$
D. 36 $mm^2$

Answer 1

The magnification formula can be used here (having I, O, v and u relation), to obtain the magnification of the image. This can be used to determine the area made by the image of the square.

Formula used:
Magnification by a concave mirror:
$m = \dfrac{I}{O} = \dfrac{v}{u}$.
Also for spherical mirrors,
$\dfrac{1}{f} = \dfrac{1}{v} + \dfrac{1}{u}$
where all the symbols used here have their usual meanings.

Complete step by step answer:
We are given that the object distance is u = - 25 cm and focal length for the given concave mirror is - 10 cm.
The image distance can be known as:
$\dfrac{1}{v} = \dfrac{1}{f} - \dfrac{1}{u}$
$\implies v = \dfrac{uf}{u - f } = \dfrac{(-25) \times (-10) }{(-25) - (-10) } = - \dfrac{50}{3}$cm.

Now, the square is placed as shown below:

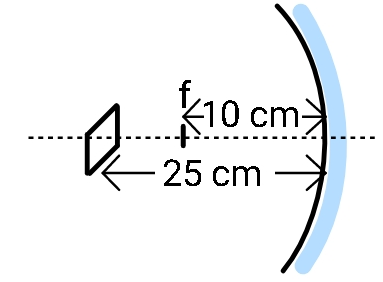
If we consider the object height to be the distance above the principal axis, we will find it to be 1.5 mm i.e., half the side of the square. By using the magnification formula we can find the amount by which this distance gets magnified. So, we may write:
$I = \dfrac{(50/3)}{25} \times 1.5 = 1$mm.

There, for the same length 1.5 mm of the object below the axis, we will get the same magnification. Therefore, the side of the square should be 2 mm for the case of image. The area will therefore be 4 $mm^2$. So, the correct answer is option (A).

Note:
We have considered here the object distance above the axis to be half the side of the square so that the definition of object height fits here. One can also do this simply by keeping the object height as it is i.e., 3 mm and noting the change or magnification that the concave mirror provides to this.