Question
Question: A square loop of length \( L = 0.2m \) and resistance \( R = 80m\Omega \) lies with one of its lengt...
A square loop of length L=0.2m and resistance R=80mΩ lies with one of its lengths along the x -axis as shown in the figure. It moves with speed V=10ms−1 in the positive x -direction in a magnetic field that is into the paper and has a magnitude that varies with x according to B=αx where α=0.2Tm−1 . The magnitude of the induced current is I ampere. Then the value of 10I is? (Neglect self-inductance of the loop)
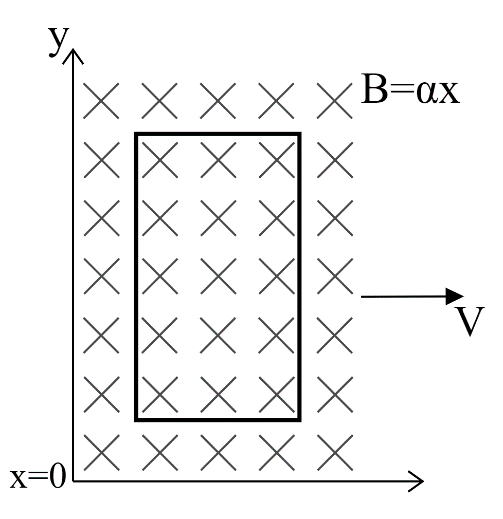
Solution
Hint : As the square loop moves along the x - axis, the flux passing through the loop changes as the strength of the magnetic field varies with x . Due to the change in flux, an emf is generated in the loop. From the emf generated and the resistance of the loop, we can find the induced current.
Complete Step By Step Answer:
Let us note down the given data as follow;
Length of loop L=0.2m
As the loop is square,
Area of the loop Area=0.2m×0.2m
∴Area=0.04m2
Resistance of the loop, R=80mΩ
The velocity of the loop, V=10ms−1
The magnitude of the magnetic field, B=0.2x
Now, the loop is moving along the x - axis. The magnitude of the magnetic field changes with the value of x .
Thus, as the loop moves forward, the magnetic field passing through the loop increases.
Thus, the magnetic flux passing through the loop changes.
The magnetic flux is calculated as,
ϕ=BAcosθ
Where, θ is the angle between the magnetic field and the area of the loop.
Here, as shown in the figure the magnetic field is going inside the paper and is perpendicular to the loop, and so θ=0
∴ϕ=BA
∴ϕ=(0.2Tm−1)x×0.04m2
Without considering the units,
∴ϕ=0.008x
∴ϕ=[(8×10−3)x]Tm2
By Faraday’s law of induction, when the flux changes inside a loop, an emf equal to the negative rate of change of magnetic flux is induced.
As we only want the magnitude, we will ignore the negative sign,
ε=dtdϕ
∴ε=dtd[(8×10−3)x]
The constant value comes out of the derivation,
∴ε=8×10−3dtdx
Now, the rate of change of position is equal to the velocity
∴ε=8×10−3×V
Substituting the given value of velocity
∴ε=8×10−3×10ms−1
Without considering the units,
∴ε=8×10−3×10
∴ε=8×10−2V
Now, by ohm’s law, the ratio of the emf to the resistance of the loop is equal to the induced current.
∴I=Rε
Substituting the given values,
∴I=80mΩ8×10−2V
Without considering the units,
∴I=80×10−38×10−2
∴I=8×10−48×10−2
Canceling the common terms and shifting the power to the numerator,
∴I=100A
Here, we need to find the value of 10A
∴10I=1000A .
Note :
For the emf induced by moving the loop in the magnetic field, we have a derived formula ε=Blv , where l is the length of the loop. But here we cannot use the direct formula, as the derived formula is for a uniform magnetic field and here we are given a varying magnetic field.
