Question

A square loop of area $2.5 \times {10^{ - 3}}{m^2}$ and having 100 turns with a total resistance of 100 $\Omega$ is moved out of a uniform magnetic field of $0.04T$ in 1 s with a constant speed. Then the work done in pulling the loop is:

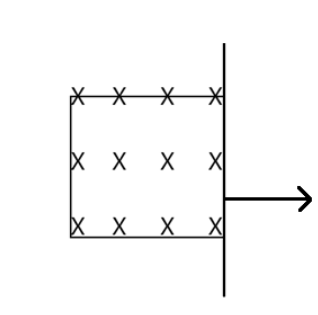
(A) 0
(B) 1 mJ
(C) $1\mu J$
(D) $0.1mJ$

Answer 1

The work done in pulling the loop is the work done against the emf induced in the loop. It would be equal in magnitude to the electrical work done in the conductor.

Formula used: In this solution we will be using the following formulae;
$e = NBlv$ where $e$ is the electromotive force or emf induced in a conductor moving in a magnetic field, $N$ is the number of turns of the conductor $l$ is the length of the conductor parallel to the direction of the velocity, and $v$ is the velocity.
$W = \dfrac{{{e^2}}}{R}$ where $W$ is the electrical work done in a conductor and $R$ is the resistance of the conductor.
$A = {l^2}$ where $A$ is the area of the square loop, and $l$ is the length of the side.

Complete Step-by-Step solution:
To calculate the work done in pulling the loop, we recall that the emf induced in the conductor which is moving in a magnetic field can be given by
$e = NBlv$ where $N$ is the number of turns of the conductor$l$ is the length of the conductor parallel to the direction of the velocity, and $v$ is the velocity.
Now, we must calculate the length of the sides and the velocity of the movement.
Area of a square is
$A = {l^2}$ hence, from calculating the length from given area, we have
$l = \sqrt {2.5 \times {{10}^{ - 3}}} = 0.05m$
Hence, to calculate $v$, we have
$v = \dfrac{l}{t} = \dfrac{{0.05}}{1} = 0.05m{s^{ - 1}}$
Hence, to calculate the emf,
$e = NBlv = 100 \times 0.4 \times 0.05 \times 0.05$
$\Rightarrow e = 0.1{\text{V}}$
Then, the work done is given
$W = \dfrac{{{e^2}}}{R} = \dfrac{{{{0.1}^2}}}{{100}}$
$\Rightarrow W = 1 \times {10^{ - 4}}{\text{J or 0}}{\text{.1mJ}}$

Hence, the correct option is D

Note: For clarity, the work done by the emf will actually be in the opposite direction as the work done by object. The moment the conductor starts to move the emf induced will tend to move the object in the opposite direction.