Question

A square is made by joining four rods each of mass M and length L. Its moment of inertia about an axis PQ in its plane and passing through one of its corners is?

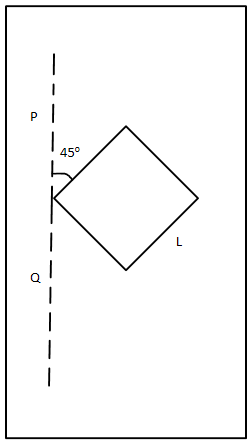
(A)$6M{L^2}$
(B) $\dfrac{2}{3}M{L^2}$
(C) $\dfrac{8}{3}M{L^2}$
(D) $\dfrac{{10}}{3}M{L^2}$

Answer 1

When a rod rotates about an end such that the rod makes angle θ with the axis of rotation, its moment of inertia is given by $I = \dfrac{{M{L^2}{{\operatorname{Sin} }^2}\theta }}{3}$, where M denotes the mass of the rod and L denotes its length.

Complete step by step solution:
If we name the four corners of the squares as A, B, C, and D. Then we can call the four rods to be AB, BC, CD and DA.

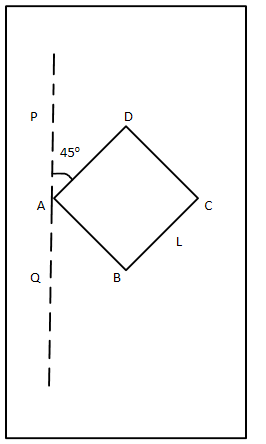
From the diagram it is clear that the diagonal BD is parallel to the axis PQ.
Consider an axis passing through corners B and D, then by symmetry moment of inertia of all the rods about this axis should be the same, since each rod makes angle 45o with the axis BD and the axis is passing through one of the ends of each rod.
If moment of inertia of each rod about the axis BD is I then I can be calculated as
$I = \dfrac{{M{L^2}{{\operatorname{Sin} }^2}\theta }}{3}$,
Putting the value of θ
$I = \dfrac{{M{L^2}{{\operatorname{Sin} }^2}{{45}^o}}}{3}$
$I = \dfrac{{M{L^2}}}{6}$
So the moment of inertia of all the rods together will be
${I_{BD}} = 4I$,
${I_{BD}} = \dfrac{{4M{L^2}}}{6}$,
${I_{BD}} = \dfrac{{2M{L^2}}}{3}$
Now applying parallel axis theorem for the system, we can write that the moment of inertia of the system about PQ will be
${I_{PQ}} = {I_{BD}} + m{d^2}$
Where m denotes the mass of the system and d denotes the distance between the axis BD and PQ
m = 4M and $d = \dfrac{a}{{\sqrt 2 }}$
Putting these values and the value of IBD, we get
${I_{PQ}} = \dfrac{{2M{L^2}}}{3} + 4M{\left( {\dfrac{L}{{\sqrt 2 }}} \right)^2}$,
${I_{PQ}} = \dfrac{{2M{L^2}}}{3} + 2M{L^2}$,
${I_{PQ}} = \dfrac{{8M{L^2}}}{3}$
Therefore, the correct answer to the question is option : C

Note: When we wrote parallel axis theorem ${I_{PQ}} = {I_{BD}} + m{d^2}$, it was applicable because the axis BD passes through the centre of mass of the system. If BD didn’t pass through the COM of the system, then parallel axis theorem won't be applicable.