Question
Question: A square is made by joining four rods each of mass \( M \) and length \( L \) . Its moment of inerti...
A square is made by joining four rods each of mass M and length L . Its moment of inertia about an axis PQ, in its plane and passing through one of its corners is
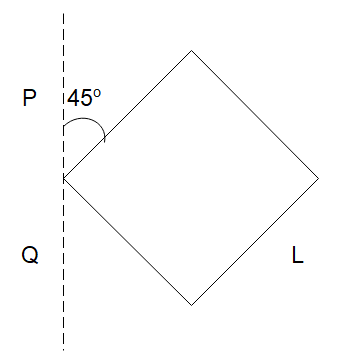
Solution
Hint : In this solution, we will first determine the moment of inertia of the rod about its diagonal that is parallel to the axis of rotation. Then, we will use the parallel axis theorem to find the net moment of inertia of the system.
Formula used: In this solution, we will use the following formulas
Moment of inertia of a rod about one of its end: I=3ML2 where M is the mass of the rod and L is its length
Parallel axis theorem: I=Ic+MR2 where IC is the moment of inertia of an object about a point and R is the distance of the point of the rotation from the axis of rotation.
Complete step by step answer:
To find the moment of inertia first let us name some points of interest in the diagram as shown below:
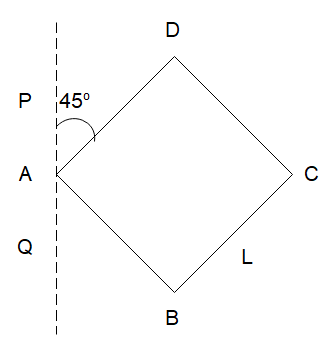
Now in this diagram, first we will find the moment of the inertia of the system about the diagonal BD of the square formed by the four rods, and then we will use the parallel axis theorem to determine the moment of inertia of the system about the axis PQ.
So, for the axis PQ, the moment of inertia of the system will be due to four rods will the moment of inertia of a rod about one of its end. And only the component of the rod perpendicular to the axis of rotation will contribute to the moment of inertia so the length of the rod will be Lsin45∘ . Hence the moment of inertia of all the four rods will be
IBD=4×3ML2sin245∘
⇒IBD=32ML2
Since we now know the moment of inertia of the system about the axis PQ, we can now use the parallel axis theorem to find the moment of inertia about the axis PQ. As the distance between the axis PQ and axis BD is equal to half the length of the diagonal of the square formed of the rods i.e. 212L=2L
We can calculate the moment of inertia as
IPQ=IBD+4M(2L)2
Which give us,
IPQ=32ML2+4M(2L)2
∴IPQ=38ML2 .
Note:
Here, we can use the parallel axis theorem because the two axes BD and PQ are parallel to each other. Also, the centre of mass of the system must pass through BD to calculate the moment of inertia directly for it which it does in this case.
