Question

A square is made by joining four rods each of mass M and length L. its moment of inertia about an axis PQ, in its plane and passing through one of its corner

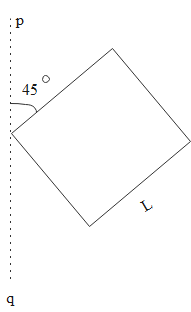
A. $6M{{L}^{2}}$
B. $\dfrac{4}{3}M{{L}^{2}}$
C. $\dfrac{8}{3}M{{L}^{2}}$
D. $\dfrac{10}{3}M{{L}^{2}}$

Answer 1

This problem is solved using the theorem of parallel axis
${{I}_{1}}={{I}_{2}}+\left( 4M \right){{r}^{2}}$
Moment of inertia is the ratio of the resultant angular momentum of the system to the angular velocity of a principal axis. That means if the angular momentum of the system is a constant, then when the moment of inertia gets smaller, the angular velocity should also increase.

Complete step-by-step answer:
First of all let us look at the moment of inertia definition. Moment of inertia is the ratio of the resultant angular momentum of the system to the angular velocity of a principal axis. That means if the angular momentum of the system is a constant, then when the moment of inertia gets smaller, the angular velocity should also increase.

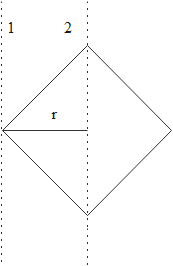
Theorem of parallel axes states that ‘the moment of inertia of a body about any axis is equal to the sums of its moment of inertia about a parallel axis passing through its center of mass and the product of its mass and the square of the perpendicular distance between the two parallel axes.’
According to this theorem,we can write that
${{I}_{1}}={{I}_{2}}+\left( 4M \right){{r}^{2}}$
Here we can see that it is a square that given so the radius $r$ will be the half of the diagonal. So the radius
$r=\dfrac{L}{\sqrt{2}}$
If the moment of inertia of each of the rod about the axis is $I$, then the value can be given as,
$I=\dfrac{M{{L}^{2}}{{\sin }^{2}}\theta }{3}$
Thus the value of moment of inertia of all the rods together will be,
${{I}_{2}}=4I$
${{I}_{2}}=4\times \dfrac{M{{L}^{2}}{{\sin }^{2}}\theta }{3}$
Therefore after substituting as per the question,
${{I}_{1}}=4\left( \dfrac{M{{L}^{2}}}{3}{{\sin }^{2}}45{}^\circ \right)+4M{{\left( \dfrac{L}{\sqrt{2}} \right)}^{2}}=\dfrac{8}{3}M{{L}^{2}}$
Hence the correct answer is $\dfrac{8}{3}M{{L}^{2}}$

So, the correct answer is “Option D”.

Note: Moment of inertia is otherwise called as the mass moment of inertia and angular mass or rotational inertia; it is in short the torque required for a particular angular acceleration about a rotational axis of a rigid body.