Question

A square is drawn by joining the mid-points of the sides of a given square. A third square is drawn inside the second square in the same way & continues indefinitely. If a side of first square is 4 cm, then the sum of the areas of all the squares is:

& (\text{A) 24} \\\ & \text{(B) 32} \\\ & \text{(C) 48} \\\ & \text{(D) 64} \\\ \end{aligned}$$

Answer 1

Let us assume a square ABCD. First, we should find the area of square ABCD. Let us assume this area is equal to A. Now we have to draw a square by joining the mid-points of square ABCD. We should find the side of the square using Pythagoras theorem. Now we have to find the area of square EFGH. Let us assume this area is equal to B. Now we have to draw a square by joining the mid-points IJKL. Now we have to find the side of the square by using Pythagoras theorem. Let us assume this area is equal to C. Now infinite squares are formed in the same pattern. Now we have to find the sum of all areas of infinite squares. Now we should find the progression in which the series is present. Based on the progression, apply the formula of sum of series.

Complete step-by-step answer:
Before solving the question, we should know that if the side of a square is equal to “a”, then the area of the square is equal to ${{a}^{2}}$.
From the question, it was given that a square is drawn by joining the mid-points of the sides of a given square. A third square is drawn inside the second square in the same way & continues indefinitely. It was also given that the side of the first square is equal to 4 cm.

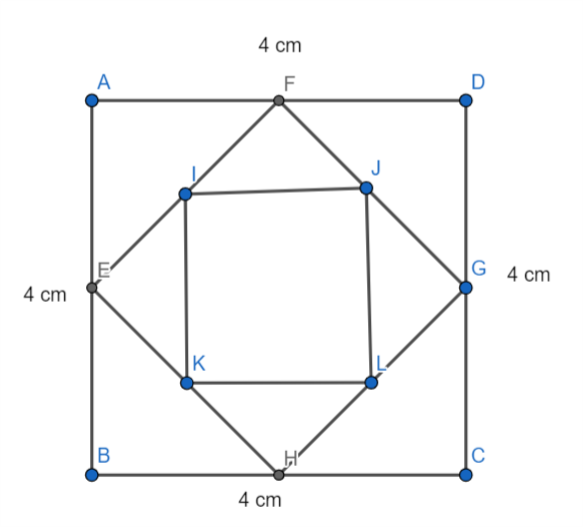
Let us assume the square is ABCD whose length is equal to 4 cm.
Now we have to find the area of square ABCD. Let us assume the area of square ABCD is equal to ${{A}_{0}}$
$\Rightarrow {{A}_{0}}={{\left( 4 \right)}^{2}}=16c{{m}^{2}}$

Now let us take mid-point on the side AB, mid-point on the side BC, mid-point on the side CD, mid-point on the side DA is E, H, G and F respectively. This will result in the square EFGH. Now we should find the side of square EFGH.
Let us assume the side of the square is equal to x.
Let us apply Pythagoras theorem in $\Delta AEF$, we get
$\Rightarrow E{{F}^{2}}=A{{E}^{2}}+A{{F}^{2}}.....(1)$
As E is the midpoint of side AB, the length of AE is equal to 2cm.
$\Rightarrow AE=2cm.....(2)$
In the similar manner, F is the midpoint of side AD. So, the length of AF is equal to 2 cm.
$\Rightarrow AF=2cm.....(3)$
Now we have to substitute equation (2) and equation (3) in equation (1), we get

& \Rightarrow E{{F}^{2}}=4+4 \\\ & \Rightarrow EF=2\sqrt{2}cm....(4) \\\ \end{aligned}$$ $$\Rightarrow x=EF=2\sqrt{2}$$ So, the length of the side of square EFGH is equal to $$2\sqrt{2}$$cm. Now we have to calculate the area of square EGH. Let us assume the area of square EFGH is equal to A. $$\begin{aligned} & \Rightarrow A={{\left( 2\sqrt{2} \right)}^{2}} \\\ & \Rightarrow A=8c{{m}^{2}} \\\ \end{aligned}$$ Now let us take mid-point on the side EF as I, mid-point on the side EG is J, mid-point on the side EH is K and mid-point on the side GK is L. This forms a square IJKL. Now we should find the side of square IJKL as y. Let us apply Pythagoras theorem in $$\Delta FIJ$$, we get $$\Rightarrow I{{J}^{2}}=F{{I}^{2}}+F{{J}^{2}}.....(5)$$ As I is the midpoint of side EF, the length of FI is equal to $$\sqrt{2}$$cm. $$\Rightarrow FI=\sqrt{2}cm.....(6)$$ In the similar manner, J is the midpoint of side GF. So, the length of FJ is equal to $$\sqrt{2}$$ cm. $$\Rightarrow FJ=\sqrt{2}cm.....(7)$$ Now we have to substitute equation (2) and equation (3) in equation (1), we get $$\begin{aligned} & \Rightarrow I{{J}^{2}}=2+2 \\\ & \Rightarrow IJ=2cm....(8) \\\ \end{aligned}$$ $$\Rightarrow x=IJ=2$$ So, the length of the side of square EFGH is equal to $$2$$cm. Now we have to calculate the area of square EGH. Let us assume the area of square EFGH is equal to B. $$\begin{aligned} & \Rightarrow B={{\left( 2 \right)}^{2}} \\\ & \Rightarrow B=4c{{m}^{2}} \\\ \end{aligned}$$ In the same way, infinite squares are drawn. Now we have to find the sum of the area of infinite squares. $$\Rightarrow {{A}_{0}}+A+B+......=(16+8+4+......)c{{m}^{2}}......(9)$$ Let us assume the sum of all the areas of infinite squares is equal to $${{A}_{\infty }}$$. $${{A}_{\infty }}=(16+8+4+......)c{{m}^{2}}......(10)$$ From the sum, it is clear that the first term is equal to 16, second term is equal to 8 and third term is equal to 4. Let us find the ratio of the first two terms. $$\dfrac{{{A}_{0}}}{A}=\dfrac{8}{16}=\dfrac{1}{2}$$ So, it is clear that the common ratio of the first two terms is equal to $$\dfrac{1}{2}$$. Now let us find the ratio of the next two terms. $$\dfrac{A}{B}=\dfrac{4}{8}=\dfrac{1}{2}$$ So, it is clear that the common ratio of next terms is equal to $$\dfrac{1}{2}$$. So, the common ratio is equal to $$\dfrac{1}{2}$$. We know that a series of terms having a common ratio, then the series is said to be in geometric progression. We know that the sum of an infinite G.P $$\left( a+ar+a{{r}^{2}}+.......\infty \right)$$ is equal to $$\dfrac{a}{1-r}$$ where a is the first term and r is the common ratio. From equation (10), it is clear that 16 is the first term and $$\dfrac{1}{2}$$ is the common ratio of the sum of series. So, we get $${{A}_{\infty }}=\dfrac{16}{1-\dfrac{1}{2}}=\dfrac{16}{\left( \dfrac{1}{2} \right)}=32$$ So, the sum of areas of all the squares is equal to 32. So, option B is correct. **Note:** Students should be careful while finding the side of the square formed by joining midpoints of squares. If a small mistake is made, then we will get a wrong value for the respective side of the square. If we get the wrong value for the side of the square, then we will get the wrong value for the area of the respective square. Even we will get the wrong side for the second square as well. This will also give a wrong value for the area of the square.