Solveeit Logo
Login

Question

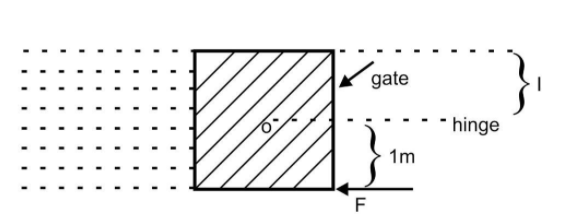
Question: A square gate of size \(2\;{\text{m}} \times 2\;{\text{m}}\) is hinged at its midpoint 0 as shown in...

A square gate of size 2  m×2  m2\;{\text{m}} \times 2\;{\text{m}} is hinged at its midpoint 0 as shown in figure. The fluid of density σ\sigma is present to the left of the square. It is held in position by an unknown force F (Given that σ\sigma is the density of fluid)

A) The torque exerted by the fluid in the upper half of the gate is σg3  Nm\dfrac{{\sigma g}}{3}\;{\text{Nm}}.
B) The torque exerted by the fluid in the upper half of the gate is 4σg3  N\dfrac{{4\sigma g}}{3}\;{\text{N}}
C) The total force exerted by the fluid on the gate is 5σg3  N\dfrac{{5\sigma g}}{3}\;{\text{N}}
D) The moment of unknown force is 4σg3  Nm\dfrac{{4\sigma g}}{3}\;{\text{Nm}}.

Explanation

Solution

In this question, first calculate the moment force exerted by the upper half of the gate then obtain the expression for the moment force exerted by the lower part of the gate. Now, from the moment of the upper and lower part of the gate, obtain the moment exerted by the unknown force.

Complete step by step answer:
In this question, the size of the square gate is 2  m×2  m2\;{\text{m}} \times 2\;{\text{m}} hinged at O and the density of the fluid is σ\sigma .
We know that the moment of force exerted by the upper half of the gate is given by
τ1=∫01σgy(2dy)(1−y){\tau _1} = \int\limits_0^1 {\sigma gy\left( {2dy} \right)} \left( {1 - y} \right)
Where σgy\sigma gy is the pressure of the fluid of depthyy, 2dy2dy is the area of a layer of thickness dydy at yy and (1−y)\left( {1 - y} \right) is the moment arm about point OO.
The density of the fluid and the acceleration due to gravity are constants so, the above expression can be written as,
τ1=2σg∫01[ydy−y2dy]{\tau _1} = 2\sigma g\int\limits_0^1 {\left[ {ydy - {y^2}dy} \right]}
Now, integrate the above equation as,
τ1=2σg[y22−y33]01{\tau _1} = 2\sigma g\left[ {\dfrac{{{y^2}}}{2} - \dfrac{{{y^3}}}{3}} \right]_0^1
After integration apply the limits which are from 00 to 11 and simplify the equation as,
⇒τ1=2σg(12−13)\Rightarrow {\tau _1} = 2\sigma g\left( {\dfrac{1}{2} - \dfrac{1}{3}} \right)
⇒τ1=2σg6\Rightarrow {\tau _1} = \dfrac{{2\sigma g}}{6}
⇒τ1=σg3\Rightarrow {\tau _1} = \dfrac{{\sigma g}}{3}
The direction of the moment τ1{\tau _1} is clockwise.
Similarly, obtain the moment force exerted by the lower half part of the gate as,
⇒τ2=∫01σg(y+1)(2dy)(y)\Rightarrow {\tau _2} = \int\limits_0^1 {\sigma g\left( {y + 1} \right)} \left( {2dy} \right)\left( y \right)
=2σg[13+12]= 2\sigma g\left[ {\dfrac{1}{3} + \dfrac{1}{2}} \right]
=5σg3= \dfrac{{5\sigma g}}{3}
Here, the direction of the moment is anticlockwise.
The moment exerted by the unknown force is calculated as,
⇒τ+τ1=τ2\Rightarrow \tau + {\tau _1} = {\tau _2}
⇒τ=τ2−τ1\Rightarrow \tau = {\tau _2} - {\tau _1}
Substitute the value of τ2{\tau _2} and τ1{\tau _1} in the above equation as,
τ=τ2−τ1\tau = {\tau _2} - {\tau _1}
⇒τ=5σg3−σg3\Rightarrow \tau = \dfrac{{5\sigma g}}{3} - \dfrac{{\sigma g}}{3}
⇒τ=4σg3  Nm\Rightarrow \tau = \dfrac{{4\sigma g}}{3}\;{\text{Nm}}

The moment of unknown force is 4σg3  Nm\dfrac{{4\sigma g}}{3}\;{\text{Nm}}. And the torque exerted by the fluid in the upper half of the gate is σg3  Nm\dfrac{{\sigma g}}{3}\;{\text{Nm}}. Therefore,option (A) and option (D) are correct.

Note:
In this problem, be careful about the direction of the moment. That is the direction of the moment due to the upper part of the gate is clockwise and the moment due to the lower part of the gate is an anti-clockwise direction.