Question

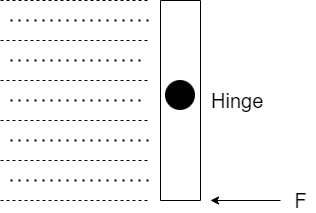
A square gate of size $1m \times 1m$ is hinged at its mid point A fluid of density $\rho$ fills the space to the left of the gate, the force F required to hold the stationary gate is

A.$\dfrac{{\rho g}}{3}$
B.$\dfrac{1}{2}\rho g$
C.$\dfrac{{\rho g}}{6}$
D.None of these

Answer 1

Recall the concept of force and torque. Force is defined as a push or a pull when an object interacts with another. A force can change the velocity or position of a body. While torque is the minimum force required to rotate the object and keep it in an angular motion.

Complete answer:
Step I:
The pressure at the bottom of the fluid will be more than at the top. Therefore the gate has a tendency to move from the bottom. To balance this, an extra force F is applied at the bottom. So consider a small element dx on which the pressure is exerted. Let the element dx be taken at a depth x.

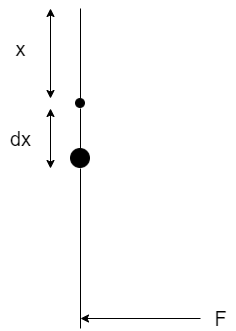
Step II:
The pressure exerted by the fluid is given by $\rho gh$
When the system is in equilibrium, the net torque acting on the hinge is zero. That is
$\Rightarrow {\tau _{net}} = 0$
Step III:
The force acting on the element dx of the gate will be
$\Rightarrow force = pressure \times area$
$Pressure = \rho gx$
$Area = 1.dx$
Therefore,
$\Rightarrow dF = \rho gx.dx$
Step IV:
The torque is the minimum force required to rotate the hinge and is obtained by the product of the force and the perpendicular distance. Also the hinge is at half distance from the whole length of the gate. So the perpendicular distance will be $x - 0.5$. So the torque about the hinge is given by
$\Rightarrow d\tau = \int {dF.(x - 0.5)}$
$\Rightarrow \int\limits_0^\tau {d\tau } = \int\limits_0^1 {\rho gx.dx.(x - 0.5)}$
$\Rightarrow \left[ \tau \right]_0^\tau = \rho g\int\limits_0^1 {({x^2} - 0.5x)dx}$
$\Rightarrow (\tau - 0) = \rho g\left[ {\dfrac{{{x^3}}}{3} - \dfrac{{0.5{x^2}}}{2}} \right]_0^1$
$\Rightarrow \tau = \rho g\left[ {(\dfrac{1}{3} - 0) - (\dfrac{{0.5}}{2} - 0)} \right]$
$\Rightarrow \tau = \rho g(\dfrac{1}{3} - \dfrac{1}{4})$
$\Rightarrow \tau = \dfrac{{\rho g}}{{12}}$
Step V:
The net torque applied in clockwise direction is given by$F(0.5)$. This is because torque is the force applied in the perpendicular direction. The force applied is $F$and the perpendicular distance is half of the length of the gate. The length of gate is $1m$, so the perpendicular distance is $0.5m$
Equating two torques,
$\Rightarrow F(0.5) = \dfrac{{\rho g}}{{12}}$
$\Rightarrow \dfrac{{5F}}{{10}} = \dfrac{{\rho g}}{{12}}$
$\Rightarrow \dfrac{F}{2} = \dfrac{{\rho g}}{{12}}$
$\Rightarrow F = \dfrac{{\rho g}}{6}$
Step VI:
The force required to hold the stationary gate is $\dfrac{{\rho g}}{6}$

Therefore Option C is the right answer.

Note:
It is to be noted that the torque is a vector quantity and has both magnitude and direction. The amount of torque decreases as the distance increases from the point of rotation. The direction of torque varies with the direction of force applied.