Question

A square gate of $1m \times 1m$ is hinged at its midpoint. A fluid of density $\rho$ fills the space to the left of the gate. The force F required to hold the gate stationary is:

A. $\dfrac{{\rho g}}{3}$
B. $\dfrac{{\rho g}}{2}$
C. $\dfrac{{\rho g}}{6}$
D. $\dfrac{{\rho g}}{8}$

Answer 1

As per Pascal's law, the change in pressure at any point in an incompressible fluid will result in uniform distribution of the applied pressure to the contact surface. It, basically, means that in a fluid, the pressure applied on the walls in contact, is uniform and it depends on the height. It is given by –
Pressure at a layer of fluid, $P = \rho gh$
where $\rho$ is the density of the fluid, g is acceleration due to gravity and the h is the height of the fluid column above the concerned layer.

Complete step-by-step answer:
Consider the hinged square gate which is holding a fluid of density $\rho$ to its left and F is the force applied to hold it in position.

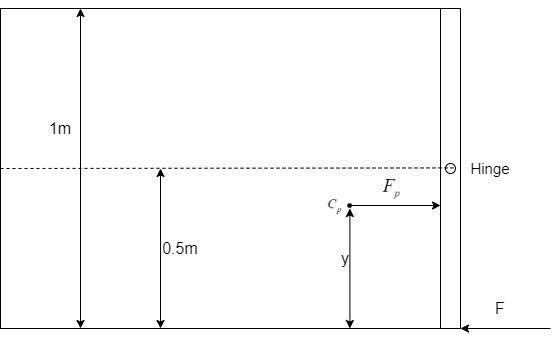
Even though the pressure on the walls of the fluid is uniform, the force due to the pressure is not uniform. The force, due to the pressure of the fluid, acts at a point in the fluid known as centre of pressure.
The centre of pressure is defined as the point at which the net total force due to the pressure of the liquid, acts on the wall containing the fluid.
Here, ${C_p}$ is the centre of pressure at a distance of y from the base and the force applied from this point is ${F_p}$.
The force ${F_p}$ causes a moment of force since it is a distance from the hinge.
${\tau _p} = {F_p}\left( {0.5 - y} \right)$
Area of the wall, $A = 1m \times 1m = 1{m^2}$
To calculate ${F_p}$:
${F_p} = P \times A = P \times (1) = P$
Since the pressure acts uniformly on the wall, the total pressure,
$P = \int {\rho gy.dy}$
where y is the individual distance of the layer from the base.

Therefore,
${F_p} = P \\\ {F_p} = \int {\rho gy.dy} \\\$
Torque due to the force ${F_p}$ is given by –
${\tau _p} = {F_p}\left( {0.5 - y} \right) \\\ {\tau _p} = \int {\rho gy.dy} \left( {0.5 - y} \right) \\\$
Since, the value of the y varies from top of the hinge, which is 1m to the bottom base which is 0m, it turns into a definite integral with the limits 1 to 0.
Therefore,
${\tau _p} = \int\limits_1^0 {\rho gy.dy\left( {0.5 - y} \right)}$
Integrating and substituting the limits, we get the torque acting due to the force ${F_p}$:
${\tau _p} = \int\limits_1^0 {\rho gy.dy\left( {0.5 - y} \right)} \\\ \to {\tau _p} = \rho g\int\limits_1^0 {\left( {0.5 - y} \right)y.dy} \\\ \to {\tau _p} = \rho g\int\limits_1^0 {0.5y - {y^2}.dy} \\\ \to {\tau _p} = \rho g\left( {\dfrac{{0.5{y^2}}}{2} - \dfrac{{{y^3}}}{3}} \right)_1^0 \\\ \to {\tau _p} = \rho g\left( {0 - \dfrac{{0.5}}{2} + \dfrac{1}{3}} \right)_0^1 \\\ \to {\tau _p} = \rho g\left( {\dfrac{1}{3} - \dfrac{1}{4}} \right) \\\ \to {\tau _p} = \dfrac{{\rho g}}{{12}} \\\$
There is one more torque T acting about the hinge due to the force F.
$T = F \times 0.5 = F \times \dfrac{1}{2}$
For the gate to be the stationary, the net torque applied about the hinge must be zero. This means:
$\sum \tau = 0$
${\tau _p} - T = 0$ (the T is negative because it is acting in the opposite direction)
Substituting the torques, we get –
${\tau _p} - T = 0 \\\ \dfrac{{\rho g}}{{12}} - F \times \dfrac{1}{2} = 0 \\\ \to \dfrac{{\rho g}}{{12}} = F \times \dfrac{1}{2} \\\ \therefore F = \dfrac{{pg}}{6} \\\$

Hence, the correct option is Option C.

Note: This concept of centre of pressure has many applications. Some of them are : i) Design of sail of a boat: While designing the sails for the boats, they take into consideration the centre of pressure of the sail so that they can make sure the force acts at the right point by the air to move the boat. ii) Design of dams: The dam cross-section is constructed taking into account the centre of pressure so that the torque produced by the centre of pressure (as we saw in this problem) does not overturn the dam.