Question

A square frame of side $l$ carries a current $I$. The magnetic field at its centre is B. The same current is passed through a circular coil having the same perimeter as the square. The field at the center of the circular coil is $B'$. The ratio of $\dfrac{B}{B'}$ is –

& \text{A) }\dfrac{8\sqrt{2}}{{{\pi }^{2}}} \\\ & \text{B) }\dfrac{8\sqrt{2}}{{{\pi }^{3}}} \\\ & \text{C) }\dfrac{8\sqrt{2}}{\pi } \\\ & \text{D) }\dfrac{4\sqrt{2}}{{{\pi }^{2}}} \\\ \end{aligned}$$

Answer 1

We are given two structures of equal perimeter carrying equal current passing through them. We have to relate the magnetic fields associated with them using the Biot-Savart’s law from which we can find the magnetic field at the center of each coil.

Complete answer:
We need to find the magnetic field at the center of a square and magnetic field from the formula derived from the Biot-Savart’s law.
The Biot-Savart law for any element is generally given as –
$B=\dfrac{{{\mu }_{0}}Il\sin \theta }{4\pi {{r}^{2}}}$
Where, B is the magnetic field at the centre of the coil,
$I$ is the current through the loop,
$l$ is the length of the loop
r is the distance of the loop from the centre.
$\theta$ is the angle between the loop and the line joining the centre.
Now, let us consider each of the given coils.

CASE I: The square loop – Let a square loop of side $l$ have a current $I$through it.

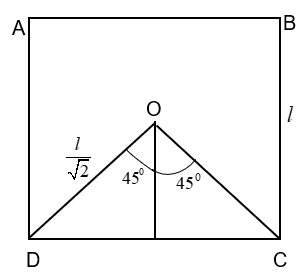
Let ABCD be the square loop. The magnetic field due to each side of the square is given by –

& B=\dfrac{{{\mu }_{0}}Il(\sin {{\theta }_{1}}+\sin {{\theta }_{2}})}{4\pi {{r}^{2}}} \\\ & \text{For all the four sides,} \\\ & B=4\times \dfrac{{{\mu }_{0}}Il(\sin {{\theta }_{1}}+\sin {{\theta }_{2}})}{4\pi {{r}^{2}}} \\\ & {{\theta }_{1}}={{\theta }_{2}}=\theta ={{45}^{0}}\text{ (from figure)} \\\ & r=\dfrac{l}{\sqrt{2}} \\\ & \Rightarrow \text{ }B=4\times \dfrac{{{\mu }_{0}}Il\sqrt{2}}{4\pi {{(\dfrac{l}{\sqrt{2}})}^{2}}} \\\ & \Rightarrow \text{ }B=\dfrac{2\sqrt{2}{{\mu }_{0}}I}{\pi l}\text{ --(1)} \\\ \end{aligned}$$ CASE II: Circular loop - Let us consider the circular loop whose perimeter is equal to that of the square with equal current. 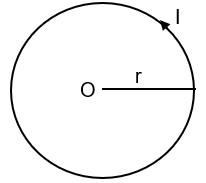 The distance from the center is given by the radius r of the circle - $$\begin{aligned} & 4l=2\pi r \\\ & \therefore \text{ }r=\dfrac{2l}{\pi } \\\ & \\\ \end{aligned}$$ Now, let us calculate the magnetic field at the centre of the loop as – $$\begin{aligned} & B'=\dfrac{{{\mu }_{0}}I}{2r} \\\ & \Rightarrow \text{ }B'=\dfrac{{{\mu }_{0}}I}{2\dfrac{2l}{\pi }}=\dfrac{{{\mu }_{0}}\pi I}{4l}\text{ --(2)} \\\ \end{aligned}$$ Now we can find the ratio between the magnetic fields B and B’ from (1) and (2) as – $$\begin{aligned} & B=\dfrac{2\sqrt{2}{{\mu }_{0}}I}{\pi l}\text{ } \\\ & \text{and,} \\\ & B'=\dfrac{{{\mu }_{0}}\pi I}{4l} \\\ \end{aligned}$$ $$\begin{aligned} & \Rightarrow \text{ }\dfrac{B}{B'}=\dfrac{\dfrac{2\sqrt{2}{{\mu }_{0}}I}{\pi l}}{\dfrac{{{\mu }_{0}}\pi I}{4l}} \\\ & \therefore \text{ }\dfrac{B}{B'}=\dfrac{8\sqrt{2}}{{{\pi }^{2}}} \\\ \end{aligned}$$ **So, the correct answer is “Option A”.** **Note:** From the observations, we can understand that the perimeter of the coil doesn’t affect the magnetic field of two orientations. The magnetic field is dependent on the closed loop, its distance from the point under consideration and the current through loop.