Question

A spy report about a suspected car reads as follows. “The car moved 2.00 km towards east, made a perpendicular left turn, ran for 500 m, made a perpendicular right turn, ran for 4.00 km and stopped". Find the displacement of the car.

Answer 1

Hint: In this question use the given information to make the figure of the motion of the car and remember to use the method of Pythagoras theorem i.e. ${\left( {hypotenuse} \right)^2} = {\left( {base} \right)^2} + {\left( {perpendicular} \right)^2}$to find the displacement of the car.

Complete step-by-step answer:
According to the given information car moving 2km towards east suddenly makes a turn to perpendicular left and after making ran of 500m it takes a perpendicular turn to right
Let’s make the figure of motion of car

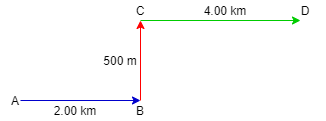
By making a point E joining point D and B such that DE is perpendicular to BE and CD also DE is parallel to CB and joining the point A to D we get figure as shown below

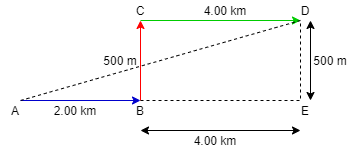
Now since CB is equal to DE therefore DE = 500m = 0.5 km and BE = 4km
So to find the displacement done by car we have to find the distance from A to D i.e. AD and
AE = AB + BE
$\Rightarrow$ AE = 2 + 4 = 6 Km
Since AED is an right angle triangle
So by the Pythagoras theorem i.e. ${\left( {hypotenuse} \right)^2} = {\left( {base} \right)^2} + {\left( {perpendicular} \right)^2}$ in triangle AED
${\left( {AD} \right)^2} = {\left( {AE} \right)^2} + {\left( {ED} \right)^2}$
Substituting the given values in the above equation
${\left( {AD} \right)^2} = {\left( 6 \right)^2} + {\left( {0.5} \right)^2}$
$\Rightarrow$ ${\left( {AD} \right)^2} = 36 + 0.25$
$\Rightarrow$ ${\left( {AD} \right)^2} = 36.25$
$\Rightarrow$ $AD = \sqrt {36.25}$
$\Rightarrow$AD = 6.02km
So the distance from A to D is 6.02 km.

Hence, The displacement done by car is equal to 6.02 km

Note: In the above solution we used the Pythagoras theorem because it is the method which explains the relation between the sides of right angles triangle and also since the path followed by the car in which the car took 2 perpendicular turns first left perpendicular turn then right perpendicular turn which gave us the idea to making a right angled triangle to the path of the car such that the displacement done by car is represented by the hypotenuse of the triangle and we can apply the Pythagoras theorem to find the displacement.