Question
Question: A spring of spring constant k is compressed by an amount of x and a mass m is just placed in contact...
A spring of spring constant k is compressed by an amount of x and a mass m is just placed in contact with it and released. Calculate minimum value of x for which the mass m completes the vertical circle in the circular track.
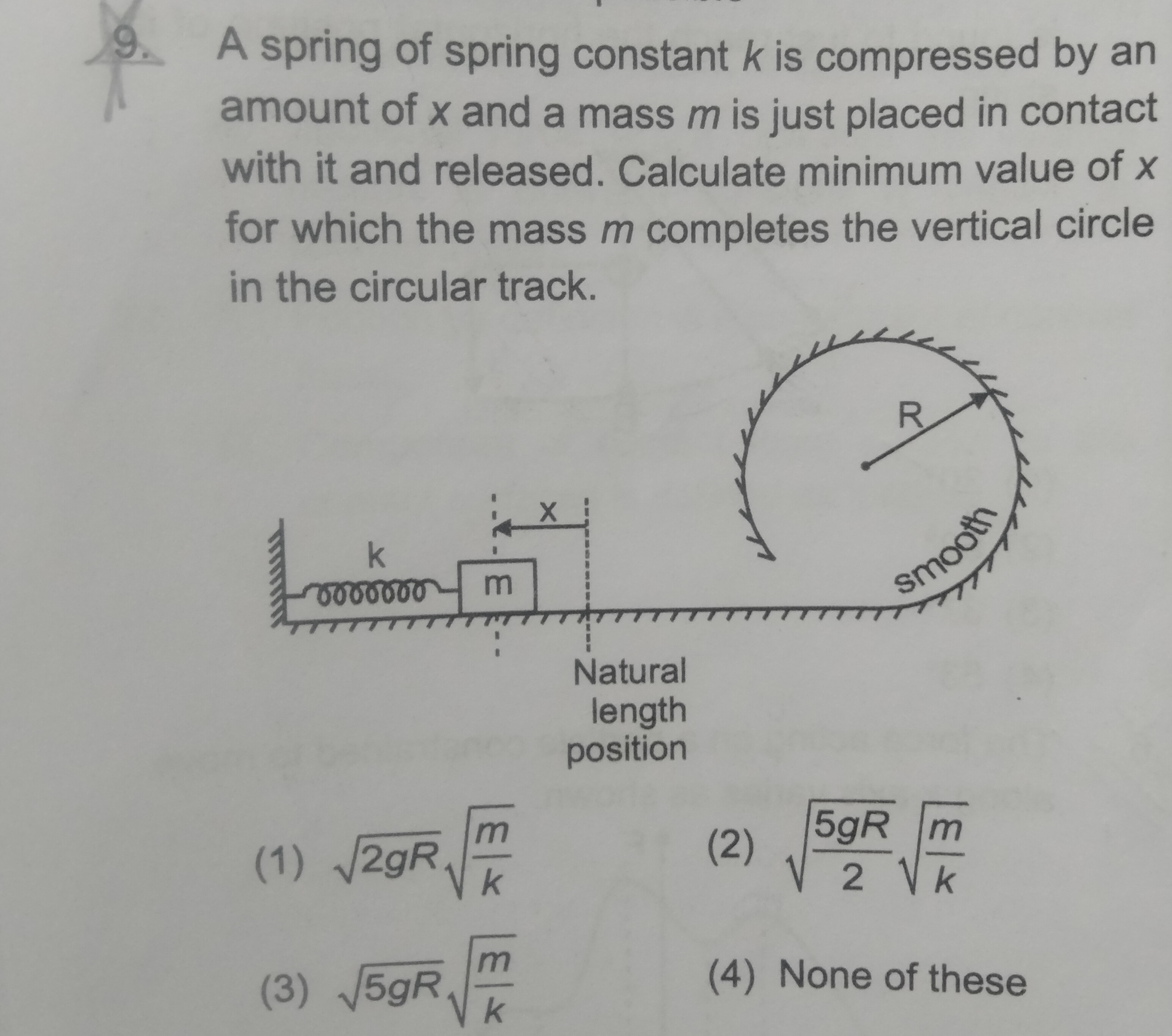
2gRkm
25gRkm
5gRkm
None of these
5gRkm
Solution
To solve this problem, we need to apply the principle of conservation of mechanical energy and the condition for completing a vertical circular motion.
Step 1: Energy stored in the spring and initial velocity of the mass. When the spring is compressed by an amount 'x', the potential energy stored in it is given by: PEspring=21kx2
When the mass 'm' is released, this potential energy is converted into kinetic energy of the mass as it leaves the spring at the natural length position. Let the velocity of the mass at this point (which is also the bottom of the circular track) be vbottom. By conservation of energy: 21kx2=21mvbottom2
This gives us the relationship between 'x' and vbottom: vbottom2=mkx2 (Equation 1)
Step 2: Condition for completing a vertical circle. For a mass to complete a vertical circle of radius 'R' on a smooth track, the minimum velocity at the highest point of the circle (the top of the loop) must be gR. Let this velocity be vtop. So, vtop=gR
Step 3: Conservation of energy in the circular track. Now, we apply the conservation of mechanical energy between the bottom of the circular track and the top of the circular track. Let the bottom of the track be the reference level for potential energy (PE=0). At the bottom: Kinetic Energy (KEbottom) = 21mvbottom2 Potential Energy (PEbottom) = 0 Total Energy at bottom (Ebottom) = 21mvbottom2
At the top: The height of the top of the circle from the bottom is 2R. Kinetic Energy (KEtop) = 21mvtop2 Potential Energy (PEtop) = mg(2R) Total Energy at top (Etop) = 21mvtop2+mg(2R)
By conservation of mechanical energy (Ebottom=Etop): 21mvbottom2=21mvtop2+mg(2R)
Step 4: Substitute vtop and solve for vbottom. Substitute vtop=gR into the energy conservation equation: 21mvbottom2=21m(gR)2+mg(2R) 21mvbottom2=21mgR+2mgR 21mvbottom2=21mgR+24mgR 21mvbottom2=25mgR Multiply by 2: mvbottom2=5mgR vbottom2=5gR (Equation 2)
Step 5: Equate the expressions for vbottom2 and solve for x. From Equation 1, we have vbottom2=mkx2. From Equation 2, we have vbottom2=5gR. Equating these two expressions: mkx2=5gR Now, solve for x: x2=k5mgR x=k5mgR This can be written as: x=5gRkm
Comparing this result with the given options: (1) 2gRkm (2) 25gRkm (3) 5gRkm (4) None of these
The calculated value of x matches option (3).
The final answer is (3)
Explanation of the solution:
- Energy Conversion (Spring to Kinetic): The potential energy stored in the compressed spring (21kx2) is entirely converted into kinetic energy (21mvbottom2) of the mass as it leaves the spring at the bottom of the track. This gives vbottom2=mkx2.
- Vertical Circle Condition: For the mass to complete the vertical circle, its minimum speed at the highest point of the loop (height 2R) must be vtop=gR.
- Energy Conservation (Bottom to Top of Loop): Apply conservation of mechanical energy between the bottom of the loop and the top of the loop. The initial kinetic energy at the bottom (21mvbottom2) is converted into kinetic energy (21mvtop2) and gravitational potential energy (mg(2R)) at the top.
- Solve for vbottom: Substituting vtop=gR into the energy conservation equation yields 21mvbottom2=25mgR, which simplifies to vbottom2=5gR.
- Solve for x: Equating the two expressions for vbottom2 (from step 1 and step 4) gives mkx2=5gR. Solving for x, we get x=5gRkm.
Answer: The minimum value of x is 5gRkm. The correct option is (3).
