Question
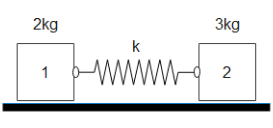
Question: A spring of length \(15{\text{ cm}}\) is connected to the masses as shown in the figure and compress...
A spring of length 15 cm is connected to the masses as shown in the figure and compressed 5 cm. The system is released on a smooth horizontal surface. Find the speed of each block when the spring is again at its free length. The force constant for spring is 2100 Nm−1.
Solution
We need to know about Hooke's law and Newton’s third law motion to solve such problems. Also, we should be clear about the concepts of potential and kinetic energy in a spring and the relation with the spring constant.
Complete step by step answer:
Since no external force is applied the centre of mass will have zero acceleration and zero velocity since its initial and final velocity is zero. Now let us assume that the velocity of mass 1 is v1 and the velocity of mass 2 is v2. We can derive a relation from both the velocity as follows
2v1−3v2 (since the centre of mass has zero acceleration)
⇒2v1=3v2−−−−−(1)
When the spring was compressed it had some potential energy which will be converted into kinetic energy when the spring is released. We know that the potential energy of a spring having spring constant k is 21kx2.
Therefore,
21kx2=21mv12+21mv22
Substituting the values, we get
21×2100×(1005)2=21×2×v12+21×3×v22
⇒821=21(2×v12+3×v22)
From equation (1) we get
v2=32v1
Therefore substituting the value, we get
⇒421=(2×v12+94v12)
⇒421=310v12
Making velocity the subject of the equation,
⇒v12=4063
⇒v1=4063
Now in equation (1), we get
∴v2=234063
Thus we get the values of the speed of each mass when the spring is in its free length.
Note: We should note that the spring constant of a spring is defined as the force required per unit of extension of the spring. The larger the constant of spring the less will be its extension under application of a given force. The potential energy stored in the spring is converted to kinetic energy upon extension.
