Question

A spring of force constant k is cut into lengths of ration 1 : 2 : 3. They are connected in series and the new force constant is k’. Then they are connected in parallel and force constant is k’’. Then k’: k’’ is

Answer 1

When a number of springs are connected in an orderly fashion the system acts as a new single spring with new spring force constant. This new spring force constant depends on the force constants of individual springs and their arrangement. Series and Parallel are two important arrangement and the formulae for their resulting force constant are given below

Formula used:
$\dfrac{1}{{{k}_{s}}}=\dfrac{1}{{{k}_{1}}}+\dfrac{1}{{{k}_{2}}}+\dfrac{1}{{{k}_{3}}}$
${{k}_{p}}={{k}_{1}}+{{k}_{2}}+{{k}_{3}}$

Complete step-by-step answer:
When a number of springs are connected in an orderly fashion the system acts as a new single spring with new spring force constant. This new spring force constant depends on the force constants of individual springs and their arrangement.

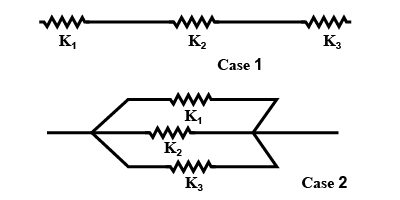
If the springs of force constants ${{k}_{1}}$, ${{k}_{2}}$and ${{k}_{3}}$are connected in series, i.e. the end of last spring and the beginning end of next spring are connected then the new force constant ${{k}_{s}}$is given by
$\dfrac{1}{{{k}_{s}}}=\dfrac{1}{{{k}_{1}}}+\dfrac{1}{{{k}_{2}}}+\dfrac{1}{{{k}_{3}}}$
And the same springs are connected in parallel, i.e. the front and last ends of all springs touch then the new spring constant ${{k}_{p}}$ is

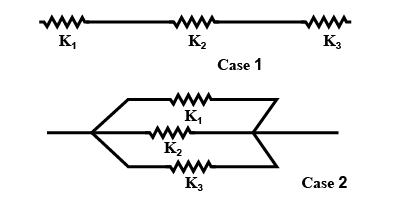
${{k}_{p}}={{k}_{1}}+{{k}_{2}}+{{k}_{3}}$
Coming to the question at hand, the ratios of the three force constants of the springs are given to be 1 : 2 : 3. Keeping the ratios constant we can assume the force constants to be
k, 2k and 3k
Now,
They are first connected in series and k’ is the new spring constant. We already know that in series $\dfrac{1}{{{k}_{s}}}=\dfrac{1}{{{k}_{1}}}+\dfrac{1}{{{k}_{2}}}+\dfrac{1}{{{k}_{3}}}$
Plugging in the values

& \dfrac{1}{{{k}_{s}}}=\dfrac{1}{{{k}_{1}}}+\dfrac{1}{{{k}_{2}}}+\dfrac{1}{{{k}_{3}}} \\\ & \Rightarrow \dfrac{1}{k'}=\dfrac{1}{k}+\dfrac{1}{2k}+\dfrac{1}{3k} \\\ & \Rightarrow \dfrac{1}{k'}=\dfrac{11}{6k} \\\ & \Rightarrow k'=\dfrac{6k}{11} \\\ \end{aligned}$$ So, $$k'=\dfrac{6k}{11}$$ Then the springs are connected in parallel and the new spring constant is k’’. Plugging in the values $$\begin{aligned} & {{k}_{p}}={{k}_{1}}+{{k}_{2}}+{{k}_{3}} \\\ & \Rightarrow k''=k+2k+3k \\\ & \Rightarrow k''=6k \\\ \end{aligned}$$ So, $$k''=6k$$ We now need to find the ratio of the two new spring constants $$k':k''$$ $$\begin{aligned} & \dfrac{k'}{k''}=\dfrac{\dfrac{6k}{11}}{6k}=\dfrac{1}{11} \\\ & \Rightarrow k':k''=1:11 \\\ \end{aligned}$$ So, k’: k’’ is 1:11, That is our answer. **Note:** The formulae for series and parallel arrangements of springs i.e. $$\dfrac{1}{{{k}_{s}}}=\dfrac{1}{{{k}_{1}}}+\dfrac{1}{{{k}_{2}}}+\dfrac{1}{{{k}_{3}}}$$ and $${{k}_{p}}={{k}_{1}}+{{k}_{2}}+{{k}_{3}}$$ can be extended to any number of springs connected in the same fashion. Most of the spring arrangement systems we will encounter will comprise these two basic arrangements only and can be solved using the given formulae.