Question

A spring of force constant $k$ is cut into lengths of ratio $1:2:3$ . They are connected in series and the new force constant is $k'$ . Then they are connected in parallel and the force constant is $k''$ . Then $k':k''$ is:
$\left( A \right)1:14 \\\ \left( B \right)1:6 \\\ \left( C \right)1:9 \\\ \left( D \right)1:11 \\\$

Answer 1

Hint : In order to solve this question, we are going to first let the three constants in which the cut spring is divided and draw a diagram to depict the situation. Then, by using the parallel and the series combination for the three parts of the spring and finding $k'$ and $k''$ , we can compute their ratio.
For a series combination of three springs of force constants ${k_1}$ , ${k_2}$ ${k_3}$ ,
$\dfrac{1}{{k'}} = \dfrac{1}{{{k_1}}} + \dfrac{1}{{{k_2}}} + \dfrac{1}{{{k_3}}}$
For a parallel combination,
${k_1} + {k_2} + {k_3}$

Complete Step By Step Answer:
Let ${k_1}$ , ${k_2}$ ${k_3}$ be the spring constants of the new springs so obtained after the spring with constant $k$ is cut.

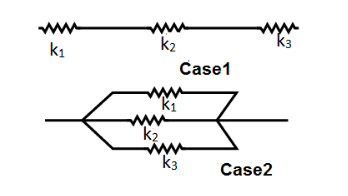
As the spring is cut in the lengths of the ratio $1:2:3$ , so the spring constant of each part is the ratio part times $k$ . Now, in the series combination, we have, the spring constant $k'$ obtained as:
$\dfrac{1}{{k'}} = \dfrac{1}{k} + \dfrac{1}{{2k}} + \dfrac{1}{{3k}}$
Solving this equation, we get
\dfrac{1}{{k'}} = \dfrac{{6 + 3 + 2}}{{6k}} = \dfrac{{11}}{{6k}} \\\ \Rightarrow k' = \dfrac{{6k}}{{11}} \\\
For the spring parts connected in the parallel, the spring constants are added directly to get the equivalent spring constant.
Thus, the spring constant $k''$ can be obtained as:
$k'' = k + 2k + 3k = 6k$
Thus, the ratio of the equivalent spring constants $k':k''$ can be obtained as:
$k':k'' = \dfrac{{6k}}{{11}}:6k = 1:11$
Hence the equivalent force constant for the parallel combination is $11$ times the spring constant for the series combination.
Thus, option $\left( D \right)1:11$ is the correct answer.

Note :
Two or more springs are said to be in series when they are connected end-to-end or point to point, and it is said to be in parallel when they are connected side-by-side; in both cases, so as to act as a single spring. Remember that in series combination, the spring constant always decreases for the spring.