Question

A spring of force constant k$= 300\,N/m$ connects two blocks having masses $2\,kg$ and $3\,kg,$ lying on a smooth horizontal plane. If the spring block system is released from a stretched position, find the number of complete oscillations in $1$ minute take $\pi = \sqrt {10}$
$\ A.44 \\\ B.150 \\\ C.34 \\\ D.55 \\\ \$

Answer 1

First we will calculate oscillation in one second i.e. its time period by formula $T = 2\pi \sqrt {\dfrac{m}{k}}$ where m is equivalent mass of system, then we will calculate oscillations for $60$ seconds i.e. one minute.

Complete step by step answer:
Given that,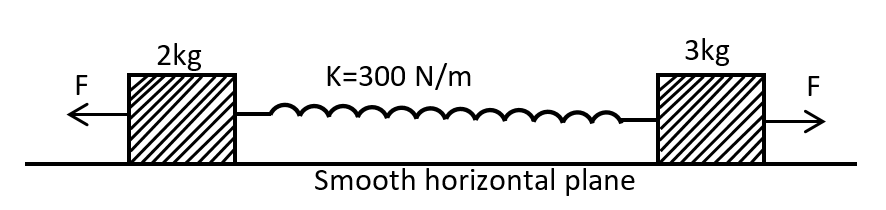
$\ {m_1} = 2\,kg \\\ {m_2} = 3\,kg \\\ k = 300\,N/m \\\ \$
Time period of oscillation of spring is given by
$= T = 2\pi \sqrt {\dfrac{m}{k}}$
Here equivalent mass is m

= \dfrac{{{m_1} \times {m_2}}}{{{m_1} + {m_2}}} \\\ m = \dfrac{{2 \times 3}}{{2 + 3}} \\\ = \dfrac{6}{5}\,kg \\\ T = 2\pi \sqrt {\dfrac{6}{{5 \times 300}}} \\\ = 2\sqrt {\dfrac{{6 \times 10}}{{5 \times 300}}} \\\ = \dfrac{2}{5} \\\ \ $$ So, oscillations in one second $ = \dfrac{5}{2}$ Oscillation in $1$ minute or $$60$$ seconds $\dfrac{5}{2} \times 60 = 150$ **So, the correct answer is “Option B”.** **Note:** (i) The calculations are done on the basis that spring is massless. If in any question spring of mass is given then consideration has to be given to that mass also. (ii) Take care to note whether oscillations are asked in one minute or one second.