Question

A spring of force constant $\alpha$ has two blocks of the same mass $M$ connected to each end of the spring as shown in the figure. Same force $f$ is applied of each end of the spring, If the masses are released, then the period of vibration is:

(A) $2\pi \sqrt {\dfrac{M}{{2\alpha }}}$
(B) $2\pi \sqrt {\dfrac{M}{\alpha }}$
(C) $2\pi \sqrt {\dfrac{{2\alpha M}}{{{\alpha ^2}}}}$
(D) $2\pi \sqrt {\dfrac{{2{\alpha ^2}}}{{2\alpha }}}$

Answer 1

The force applied on a force is given by, $F = kx$ and the Time period of the spring’s vibration is given by, $T = 2\pi \sqrt {\dfrac{M}{k}}$ . But when the forces on a body are equal and opposite to each other the net force of the body becomes zero. Hence consider the spring to be 2 springs from its centre of length $\dfrac{l}{2}$ each.

Formulas used
We will be using the formula for restoring force of a spring which is given by, $F = kx$ , where $F$ is the restoring force, $k$ is the force constant of the spring given, $x$ is the extension experienced on the spring.
We will also be using the formula $T = 2\pi \sqrt {\dfrac{M}{k}}$ where $T$ will be the time period of motion, $M$ will be the mass of the spring, and $k$ will be the spring constant.

Complete Step by Step answer
We know that the spring undergoes simple harmonic motion, and has characteristics like time period, and frequency. Also, we know that when a spring is being applied in a direction it returns back to its initial position, the force that it takes to restore its initial position is called a restoring force.
Here the restoring force is given by, $F = \alpha x$ where $\alpha$ is the spring force constant. Since the only force acting on the spring here is $f$ we can say that $f = \alpha x$ . Also, since equal and opposite forces act on the spring from either side, the net force will be zero.
So that we can consider the spring to be cut at the centre of the spring such that we have two springs. Such that the two springs we have are of equal length.
We also know that when a spring of spring force constant $\alpha$ is cut into two halves the spring constant for each spring becomes, $2\alpha$ .

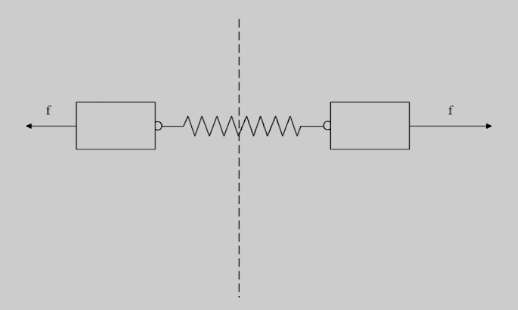
Now that we know each spring has a spring constant of $2\alpha$ . We can say that the force of each spring will be, $f = 2\alpha x$ .Also, we know that the time period of a spring is given by, $T = 2\pi \sqrt {\dfrac{M}{k}}$ , substituting, the springs force constant $k = 2\alpha$ , we get,
$T = 2\pi \sqrt {\dfrac{M}{{2{\alpha _{eq}}}}} = 2\pi \sqrt {\dfrac{{M(2\alpha + 2\alpha )}}{{2\alpha \times 2\alpha }}}$ (Since for spring in series, $\dfrac{1}{{{\alpha _{eq}}}} = \dfrac{{{\alpha _2} + {\alpha _1}}}{{{\alpha _2}{\alpha _1}}}$ )
$T = 2\pi \sqrt {\dfrac{{M(4\alpha )}}{{4{\alpha ^2}}}}$
Solving the values, we get,
$T = 2\pi \sqrt {\dfrac{M}{\alpha }}$
Thus, the time period of a spring with equal force $f$ acting on both sides is $T = 2\pi \sqrt {\dfrac{M}{\alpha }}$
Hence the correct answer will be option B.

Note
The spring constant equivalent of two springs connected in series is given by, $\dfrac{1}{{{\alpha _{eq}}}} = \dfrac{1}{{{\alpha _1}}} + \dfrac{1}{{{\alpha _2}}}$ .
However, the force ${f_{eq}}$ of the two springs in the problem connected in parallel would be ${f_{eq}} = f = 2\alpha x$