Question

A spring of force constant 800 N/m has an extension of 5 cm. Find work done in extending it from 5 cm to 15 cm?

Answer 1

When a force is by a spring on an object attached to its ends is directly proportional to the change in length of spring away from its equilibrium length, and the force is always directed towards its equilibrium position given as $F = - kx$ where constant $k$ is called spring constant and $x$ is the elongation/compression of the spring from its normal state. Spring constant is the measure of the stiffness of the spring.
In this question, a force is applied to stretch the spring from its equilibrium position; hence Elastic potential energy is stored. Elastic potential energy is the potential energy stored as a result of deformation of an elastic object which is equal to work done.

Complete step by step answer:
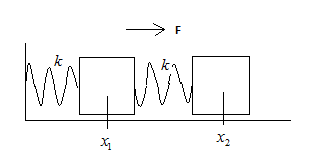
Given that the spring is extended with a constant force $k = 800N/m$
Hence the work done is stored as elastic potential energy in the spring,
The spring is extended from 5cm to 15cm which is given as
${x_1} = 5cm$
${x_2} = 15cm$

Force constant $k = 800N/m = \dfrac{{800}}{{100}}N/cm = 8N/cm$
Hence the total work done in the deformation of the spring is

$$W = \dfrac{1}{2}k\left( {x_2^2 - x_1^2} \right) \\\ = \dfrac{1}{2} \times 8 \times \left( {{{\left( {15} \right)}^2} - {5^2}} \right) \\\ = \dfrac{1}{2} \times 8 \times \left( {225 - 25} \right) \\\ = \dfrac{1}{2} \times 8 \times 200 \\\ = 800N/cm \\\$$

This can be written as:
$W = 800N/cm = 8N/m = 8J$
Hence the total work done in the extension of the spring from 5cm to 15cm is equal to $8J$

Note:
When a spring is stretched or compressed, its length changes by an amount $x$ from its equilibrium length, then it exerts a force $F = - kx$ in the direction towards the equilibrium.