Question
Question: A spring mass system is held at rest with the spring relaxed of a height h above the ground. The min...
A spring mass system is held at rest with the spring relaxed of a height h above the ground. The minimum value of h for which the system has a tendency to rebound after hitting the ground is (assume zero coefficient of restitution for tower block and ground).
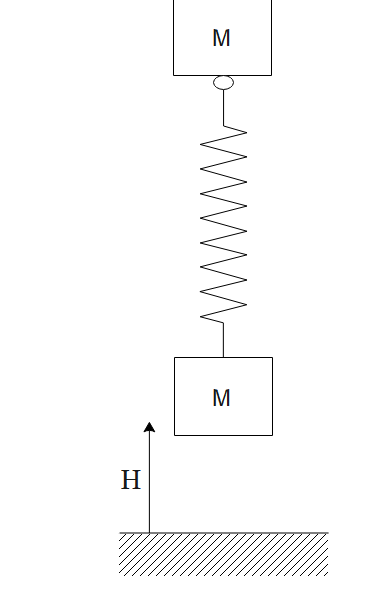
a)k2mgb)k3mgc)2k3mgd)k6mg
Solution
Let us first find out the velocity of the block when it hits the ground using the conservation of energy. Also, the compression must be such that it must lift the block again. Apply this condition and find out the minimum compression. Finally, apply conservation of energy to find the value of h at initial and final points.
Formula used:
21mv2=mgh⇒kx=mg
Complete answer:
Let’s find the velocity of the block just before it hits the ground,
21mv2=mgh⇒v=2gh...(1)
Next, for minimum compression,
kx=mg⇒x=kmg
Next, applying work energy theorem for final conditions,
21mv2+0=21kx2+mgx⇒21m(2gh)=2kmg×mg+kmg×mg⇒2mgh=k3m2g2⇒h=2k3mg
So, the correct answer is “Option C”.
Additional Information:
In a spring mass system, there will not be any external forces acting on them. A system of masses connected by springs is a classical system with several degrees of freedom. A system consisting of two masses and three springs has two degrees of freedom. As the energy is conserved in any spring mass system, the velocity of the block at any point can be easily calculated using the energy conservation system. The motion of a mass on a spring can be described as simple harmonic motion, an oscillatory motion that follows hooke's law. The natural frequency is also known as eigen frequency, is the frequency at which a system tends to oscillate in the absence of any driving or damping force. The motion pattern of a system oscillating at natural frequency is called normal mode.
Note:
In the above question, the force due to spring or during force must be greater than the weight of the block for the block to rebound. And the minimum compression requires the spring to be equal to the weight exactly. Therefore, the force is equal to the weight of the block for minimum compression.
