Question

A spring ( $k = 100{\text{N}}{{\text{m}}^{ - 1}}$ ) is suspended in a vertical position having one end fixed at the top and the other end joined to a $2{\text{kg}}$ block. When the spring is in a non-deformed shape, the block has an initial velocity of $2{\text{m}}{{\text{s}}^{ - 1}}$ in the downward direction. The maximum elongation of the spring is $\dfrac{{\sqrt 3 + 1}}{n}{\text{meters}}$. Find the value of $n$.

Answer 1

Here, as the spring deforms and attains maximum elongation a transfer of energy takes place as the total mechanical energy of the system must be conserved. This suggests that the sum of the initial kinetic energy and the work done by gravity gets stored as the potential energy of the spring.

Formulas used:
The kinetic energy of a block is given by $KE = \dfrac{1}{2}m{v^2}$ where $m$ is the mass of the block and $v$ is its velocity.
The work done by gravity on a block suspended from a spring is given by, $W = mgx$ where $m$ is the mass of the block, $g$ is the acceleration due to gravity and $x$ is the displacement of the block.
The potential energy of a spring is given by, $PE = \dfrac{1}{2}k{x^2}$ where $k$ is the spring constant and $x$ is the displacement of the spring.

Complete step by step answer:
Step 1: Sketch the spring-block system and list the parameters mentioned in the question.

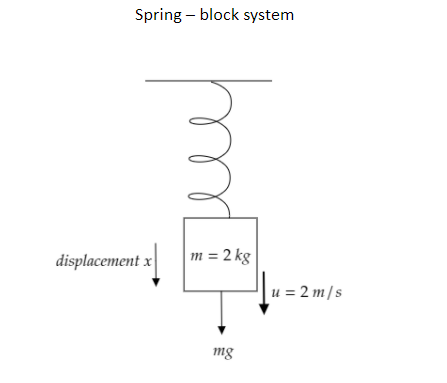
In the above figure, a block of mass $m = 2{\text{kg}}$ is suspended from a spring whose other end is fixed. The initial velocity of the black is given to be $u = 2{\text{m}}{{\text{s}}^{ - 1}}$.
The spring constant of the spring is $k = 100{\text{N}}{{\text{m}}^{ - 1}}$.
The maximum elongation of the spring is given to be $\dfrac{{\sqrt 3 + 1}}{n}{\text{meters}}$ where the value of $n$ is unknown.

Step 2: Express the relation of the initial kinetic energy of the block to find its value by substitution.
The initial kinetic energy of the block is $K{E_{initial}} = \dfrac{1}{2}m{u^2}$
Substituting values for $u = 2{\text{m}}{{\text{s}}^{ - 1}}$ and $m = 2{\text{kg}}$ in the above relation we get,
$\Rightarrow K{E_{initial}} = \dfrac{1}{2} \times 2 \times {2^2} = 4{\text{J}}$
So the initial kinetic energy of the block will be
$\Rightarrow K{E_{initial}} = 4{\text{J}}$.

Step 3: Express the work done by gravity and the potential energy of the spring when the spring suffers maximum elongation.
Let ${x_{\max }}{\text{ meters}}$ be the maximum elongation of the spring.
Then the work done by gravity on the suspended block for maximum elongation will be
$W = mg{x_{\max }}$ -------- (1)
Substituting the values for $m = 2{\text{kg}}$ and $g = 9 \cdot 8{\text{m}}{{\text{s}}^{ - 1}}$ in equation (1) We get, $W = 2 \times 9 \cdot 8{x_{\max }} = 19 \cdot 6{x_{\max }}$
So the work done by gravity for maximum elongation is $W = 19 \cdot 6{x_{\max }}$.
The potential energy of the spring for maximum elongation will be
$PE = \dfrac{1}{2}k{x_{\max }}^2$ ------- (2)
Substituting the value for $k = 100{\text{N}}{{\text{m}}^{ - 1}}$ in equation (2) we get, $PE = \dfrac{1}{2} \times 100{x_{\max }}^2 = 50{x_{\max }}^2$
So the potential energy of the spring for maximum elongation is $PE = 50{x_{\max }}^2$.

Step 4: Apply the conservation of energy to find the maximum elongation of the spring.
According to energy conservation, the initial kinetic energy and the work done by gravity gets converted to the potential energy of the spring when it suffers maximum elongation.
i.e., $K{E_{initial}} + W = PE$ --------- (3)
Substituting for $K{E_{initial}} = 4{\text{J}}$, $W = 19 \cdot 6{x_{\max }}$ and $PE = 50{x_{\max }}^2$ in equation (3) we get,
$\Rightarrow 4 + 19 \cdot 6{x_{\max }} = 50{x_{\max }}^2$
On simplifying the above equation becomes,
$\Rightarrow 12 \cdot 5{x_{\max }}^2 - 4 \cdot 9{x_{\max }} - 1 = 0$ ------- (4)
Equation (4) is quadratic in ${x_{\max }}$ and so the value of ${x_{\max }}$ is obtained by the quadratic formula ${x_{\max }} = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}$
Substituting for $a = 12 \cdot 5$, $b = - 4 \cdot 9$ and $c = - 1$ in the above formula we have,
$\Rightarrow {x_{\max }} = \dfrac{{4 \cdot 9 \pm \sqrt {{{\left( { - 4 \cdot 9} \right)}^2} + \left( {4 \times 12 \cdot 5 \times 1} \right)} }}{{2 \times 12 \cdot 5}}$
We can round off $b = - 4 \cdot 9$ as $b = - 5$ and then we have
$\Rightarrow {x_{\max }} = \dfrac{{5 \pm \sqrt {{{\left( { - 5} \right)}^2} + \left( {4 \times 12 \cdot 5 \times 1} \right)} }}{{2 \times 12 \cdot 5}}$
On evaluating, we get
$\Rightarrow {x_{\max }} = \dfrac{{5 \pm \sqrt {75} }}{{25}} = \dfrac{{1 \pm \sqrt 3 }}{5}$
i.e., the maximum elongation of the spring is ${x_{\max }} = \dfrac{{1 \pm \sqrt 3 }}{5}{\text{meters}}$

Comparing this value with the given value $\dfrac{{\sqrt 3 + 1}}{n}{\text{meters}}$ we conclude that $n = 5$.

Note:
The spring in its non-deformed shape does not possess any potential energy. But as the spring is stretched by the force of gravity and the velocity given to the block, the potential energy builds up and will be maximum when the elongation is at its maximum. If the block was not given any initial velocity, then the work done by gravity would have been equal to the potential energy of the spring by the principle of energy conservation and the maximum elongation would be smaller.